题目内容
18.若关于x的一元二次方程kx2-6x-3=0有两个不相等的实数根,则k的取值范围是k>-3且k≠0.分析 根据判别式的意义得到△=62+12k>0,然后解不等式即可.
解答 解:∵关于x的一元二次方程kx2-6x-3=0有两个不相等的实数根,
∴△=62+12k>0,且k≠0,
解得k>-3且k≠0,
故答案为:k>-3且k≠0.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
8.某商场欲购进果汁饮料和碳酸饮料共150箱,两种饮料每箱的进价和售价如下表所示.设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为w元(注:总利润=总售价-总进价).
(1)设购进碳酸饮料y箱,直接写出y与x的函数关系式为y=150-x;
(2)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过7000元,那么该商场如何进货才能获利最多?并求出最大利润.
| 果汁饮料 | 碳酸饮料 | |
| 进价(元/箱) | 55 | 38 |
| 售价(元/箱) | 75 | 45 |
(2)求总利润w关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过7000元,那么该商场如何进货才能获利最多?并求出最大利润.
9.下列说法:①平方等于4的数只有2;②若a,b互为相反数,则$\frac{b}{a}$=-1;③若|-a|=a,则(-a)3<0;④若ab≠0,则$\frac{a}{|a|}$+$\frac{b}{|b|}$的取值在0,1,2,-2这4个数中,不能得到的是0,其中正确的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.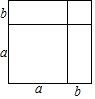 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )
 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)=a2-2ab+b2 | D. | (x+p)(x+q)=x2+(p+q)x+pq |
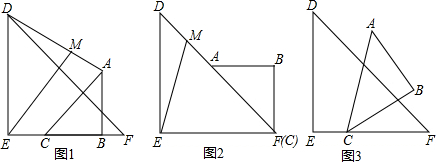
 如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度.
如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度.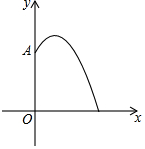 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA.O恰为水池中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,建立如图所示的平面直角坐标系时,水流喷出的高度y(m)与水平距离x(m)之间的关系式满足y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.根据以上信息,回答下列问题:
某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA.O恰为水池中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,建立如图所示的平面直角坐标系时,水流喷出的高度y(m)与水平距离x(m)之间的关系式满足y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$.根据以上信息,回答下列问题: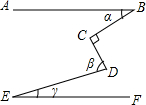 如图,AB∥EF,∠C=90°,写出α、β、γ之间的等量关系是α+β-γ=90°.
如图,AB∥EF,∠C=90°,写出α、β、γ之间的等量关系是α+β-γ=90°. 如图,点B到直线DC的距离是指线段BC的长度.
如图,点B到直线DC的距离是指线段BC的长度.