题目内容
6.如图,两等腰直角三角形ABC和DEF有一条边BC与EF在同一直线上,DE=4,AB=2.设EC=m(0≤m≤4),点M在线段AD上,且∠MEB=45°.(1)当m=4时,$\frac{AM}{DM}$=1;
(2)当m=4时,△ABC绕点C逆时针旋转90°,求$\frac{AM}{DM}$的值;
(3)当0<m<4时,△ABC绕点C逆时针旋转∂度(0<∂<90°),原题中其它条件不变,求$\frac{AM}{DM}$的值(用含m的代数式表示).
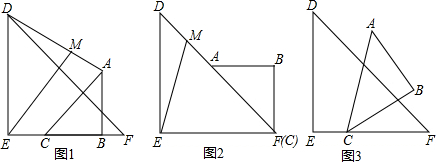
分析 (1)如图,当m=4时,C与F重合.设EM交DF于N.只要证明EM∥AF,EM⊥DF即可解决问题;
(2)只要证明△AEM∽△FEB,可得$\frac{AM}{BF}=\frac{AE}{EF}$,推出$AM=\sqrt{2}$,推出$DM=AD-AM=\sqrt{2}$,由此即可解决问题;
(3)如图3中,过B作BE的垂线交直线EM于点G,连接AG、BG.只要证明△ABG≌△CBE,推出AG=EC=m,∠AGB=∠CEB,推出∠AGM=∠DEM,推出AG∥DE,推出△AGM∽△DEM.可得$\frac{AM}{DM}=\frac{AG}{DE}=\frac{m}{4}$;
解答 解:(1)如图,当m=4时,C与F重合.设EM交DF于N.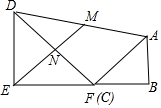
∵∠DFE=∠AFB=45°,
∴∠DFA=90°,
∵∠MEB=∠DFE=45°,
∴∠ENF=90°,
∴EM⊥DF,∠ENF=∠DFA,
∴EM∥AF,DN=NF,
∴$\frac{DM}{AM}$=$\frac{DN}{NF}$=1,
∴DM=AM.
故答案为1;
(2)如图2中,连接AE、BE.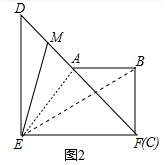
∵△ABC,△DEF均为等腰直角三角形,DE=4,AB=2,
∴EF=4,BC=2,∠DEF=90°
∴DF=$4\sqrt{2}$,AC=$2\sqrt{2}$,∠EFB=90°,
∴DF=2AC,AD=$2\sqrt{2}$,
∴点A为CD的中点,
∴EA⊥DF,EA平分∠DEF,
∴∠MAE=90°,∠AEF=45°,AE=$2\sqrt{2}$,
∵∠BEM=45°,
∴∠AEM=∠FEB,
∴△AEM∽△FEB,
∴$\frac{AM}{BF}=\frac{AE}{EF}$,
∴$AM=\sqrt{2}$,
∴$DM=AD-AM=\sqrt{2}$
∴$\frac{AM}{DM}=1$.
(3)如图3中,过B作BE的垂线交直线EM于点G,连接AG、BG.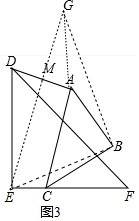
∴∠EBG=90°
∵∠BEM=45°,
∴∠EGB=∠BEM=45°,
∴BE=BG
∵△ABC为等腰直角三角形,
∴BA=BC,∠ABC=90°,
∴∠ABG=∠CBE,
∴△ABG≌△CBE,
∴AG=EC=m,∠AGB=∠CEB,
∵∠AGB+∠AGM=∠CEB+∠DEM=45°,
∴∠AGM=∠DEM,
∴AG∥DE,
∴△AGM∽△DEM.
∴$\frac{AM}{DM}=\frac{AG}{DE}=\frac{m}{4}$
点评 本题考查相似形综合题、等腰直角三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案 如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )
如图所示,点A,O,B在同一直线上,∠COA=90°,若∠1=∠2,则图中互余的角共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
| A. | -5+2=-7 | B. | (-3)2=6 | C. | $\sqrt{4}$-$\root{3}{8}$=0 | D. | 5-2x=3x |
| A. | ①③?? | B. | ???①②③ | C. | ??①③⑤ | D. | ???①②③④⑤ |
| A. | x+y=9 | B. | x+y=3 | C. | x+y=-3 | D. | x+y=-9 |