��Ŀ����
3��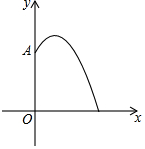 ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ�ڵ��氲װһ������OA��OǡΪˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�������ͼ��ʾ��ƽ��ֱ������ϵʱ��ˮ������ĸ߶�y��m����ˮƽ����x��m��֮��Ĺ�ϵʽ����y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$������������Ϣ���ش��������⣺
ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ�ڵ��氲װһ������OA��OǡΪˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�������ͼ��ʾ��ƽ��ֱ������ϵʱ��ˮ������ĸ߶�y��m����ˮƽ����x��m��֮��Ĺ�ϵʽ����y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$������������Ϣ���ش��������⣺��1������OA�ĸ߶�Ϊ$\frac{5}{3}$m��
��2���������ˮ�������ӵ�ˮƽ����Ϊ����mʱ��ˮ���ﵽ���߶ȣ����߶��Ƕ���m��
��3����ˮ�صİ뾶����Ҫ����mʱ������ʹ�����ˮ�����������ڳ��⣿
��4��һ����Ϊ$\frac{11}{12}$m��С�����ڳ����ھ�������Χ����m�İ뾶����ˣ���Ų�����ʹˮ��ֱ���絽���ϣ�
���� ��1��ֱ������x=0���y��ֵ�������ó���
��2��ֱ�������䷽��������κ�����ֵ�ó��𰸣�
��3������y=0ʱ�ó�x��ֵ�������ó�ˮ�صİ뾶ȡֵ��Χ��
��4������y=$\frac{11}{12}$�ó�x��ֵ�������ó��𰸣�
��� �⣺��1����x=0����y=$\frac{5}{3}$����OA=$\frac{5}{3}$m��
�ʴ�Ϊ��$\frac{5}{3}$��
��2��y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$
=-$\frac{1}{12}$��x2-8x��+$\frac{5}{3}$
=-$\frac{1}{12}$[��x-4��2-16]+$\frac{5}{3}$
=-$\frac{1}{12}$��x-4��2+3��
�������ˮ�������ӵ�ˮƽ����Ϊ4mʱ��ˮ���ﵽ���߶ȣ����߶���3m��
��3����y=0ʱ��0=-$\frac{1}{12}$��x-4��2+3��
��ã�x1=-2������������ȥ����x2=10��
��ˮ�صİ뾶����Ҫ10mʱ������ʹ�����ˮ�����������ڳ��⣻
��4����y=$\frac{11}{12}$��
��$\frac{11}{12}$=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$
��ã�x1=-1��x2=9��
���ڳ����ھ�������Χ9m�İ뾶����ˣ���Ų�����ʹˮ��ֱ���絽���ϣ�
���� ������Ҫ�����˶��κ�����Ӧ���Լ��䷽������κ�����ֵ����ȷ���ն��κ�������ֵ���ǽ���ؼ���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | -5+2=-7 | B�� | ��-3��2=6 | C�� | $\sqrt{4}$-$\root{3}{8}$=0 | D�� | 5-2x=3x |
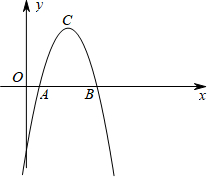 ��ͼ����֪��x�ύ�ڵ�A��1��0����B��5��0����������l�Ķ���ΪC��3��4����������l���l����x��Գƣ�
��ͼ����֪��x�ύ�ڵ�A��1��0����B��5��0����������l�Ķ���ΪC��3��4����������l���l����x��Գƣ�