题目内容
15.已知二次函数y=ax2+bx+c中y与x的部分对应值如下表所示:| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
①函数图象的对称轴是直线x=1;
②方程ax2+bx+c=0的根都不是负数;
③方程ax2+bx+c=0的根都在-1与0之间;
④方程ax2+bx+c=0的非负根在1与2之间.
分析 利用表中所给数据可求得二次函数解析式,再逐个判断即可.
解答 解:
由题意可知x=-1时y=6,x=0时y=-3,x=1时y=-4,
∴$\left\{\begin{array}{l}{a-b+c=6}\\{c=-3}\\{a+b+c=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=4}\\{b=-5}\\{c=-3}\end{array}\right.$,
∴二次函数解析式为y=4x2-5x-3,
∴抛物线对称轴为直线x=-$\frac{-5}{2×4}$=$\frac{5}{8}$,故①错误;
在y=4x2-5x-3中,令y=0可得4x2-5x-3=0,解得x1=$\frac{5+\sqrt{73}}{8}$,x2=$\frac{5-\sqrt{73}}{8}$,
∵8<$\sqrt{73}$<9,
∴1<x1<2,-1<x2<0,
∴②错误,③④正确;
综上可知错误的有①②,
故答案为:①②.
点评 本题主要考查二次函数的性质,利用待定系数法求得抛物线解析式是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.用配方法解方程x2+6x-1=0,配方后的方程是( )
| A. | (x+3)2=10 | B. | (x-3)2=10 | C. | (x+3)2=8 | D. | (x-3)2=8 |
5.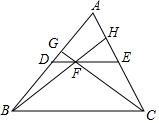 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
6.已知某圆锥的底面圆的半径r=2cm,将圆锥侧面展开得到一个圆心角θ=120°的扇形,则该圆锥的母线长l为( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
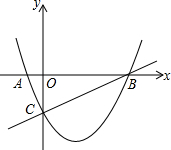 如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴的交点,连接AC.
如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴的交点,连接AC. 如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.
如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.