题目内容
5.用配方法解方程x2+6x-1=0,配方后的方程是( )| A. | (x+3)2=10 | B. | (x-3)2=10 | C. | (x+3)2=8 | D. | (x-3)2=8 |
分析 先把常数项移项,再方程两边同加上一次项系数一半的平方,再配方即可.
解答 解:x2+6x-1=0,
移项得x2+6x=1,
方程两边同加上9得x2+6x+9=10,
配方得(x+3)2=10,
故选A.
点评 本题考查了用配方法解一元二次方程,掌握用配方法解一元二次方程的步骤是解题的关键.

练习册系列答案
相关题目
15.已知a、b是方程x2-4x+2=0的两个根,则a2-2a+2b的值为( )
| A. | -4 | B. | 6 | C. | -8 | D. | 8 |
13.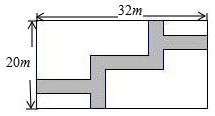 如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
 如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )| A. | (20+x)(32-x)=540 | B. | (20-x)(32-x)=100 | C. | (20-x)(32-x)=540 | D. | (20+x)(32-x)=540 |
10.一艘船顺流航行90千米与逆流航行60千米所用的时间相等,若水流的速度是2千米/时,求船在静水中的速度.设船在静水中的速度为x千米/时,则可列出的方程为( )
| A. | $\frac{90}{x+2}$=$\frac{60}{x-2}$ | B. | $\frac{90}{x-2}$=$\frac{60}{x+2}$ | C. | $\frac{90}{x}$+2=$\frac{60}{x}$ | D. | $\frac{60}{x}$+2=$\frac{90}{x}$ |
14.已知a是方程x+3x-4=0的一个根,则代数式2a2+4a+2等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
15.已知二次函数y=ax2+bx+c中y与x的部分对应值如下表所示:
则下列说法中错误的是①②
①函数图象的对称轴是直线x=1;
②方程ax2+bx+c=0的根都不是负数;
③方程ax2+bx+c=0的根都在-1与0之间;
④方程ax2+bx+c=0的非负根在1与2之间.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
①函数图象的对称轴是直线x=1;
②方程ax2+bx+c=0的根都不是负数;
③方程ax2+bx+c=0的根都在-1与0之间;
④方程ax2+bx+c=0的非负根在1与2之间.



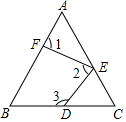 如图,直线AB、DE被EF 所截,∠1和∠2是内错角;
如图,直线AB、DE被EF 所截,∠1和∠2是内错角;