题目内容
3.在$\sqrt{2}$,-1,-3,0,1这组实数中,最小的是-3,最大的是$\sqrt{2}$,绝对值最小的是0.分析 根据任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小可得答案.
解答 解:在$\sqrt{2}$,-1,-3,0,1这组实数中,最小的是-3,最大的是$\sqrt{2}$,绝对值最小的是0,
故答案为:-3;$\sqrt{2}$;0.
点评 此题主要考查了实数的比较大小,关键是掌握实数大小比较的法则.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
13.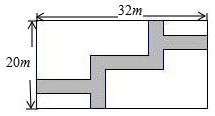 如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
 如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )| A. | (20+x)(32-x)=540 | B. | (20-x)(32-x)=100 | C. | (20-x)(32-x)=540 | D. | (20+x)(32-x)=540 |
14.已知a是方程x+3x-4=0的一个根,则代数式2a2+4a+2等于( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
11.如果不等式3x-m≤0有3个正整数解,那么m的取值不可以是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
15.已知二次函数y=ax2+bx+c中y与x的部分对应值如下表所示:
则下列说法中错误的是①②
①函数图象的对称轴是直线x=1;
②方程ax2+bx+c=0的根都不是负数;
③方程ax2+bx+c=0的根都在-1与0之间;
④方程ax2+bx+c=0的非负根在1与2之间.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
①函数图象的对称轴是直线x=1;
②方程ax2+bx+c=0的根都不是负数;
③方程ax2+bx+c=0的根都在-1与0之间;
④方程ax2+bx+c=0的非负根在1与2之间.
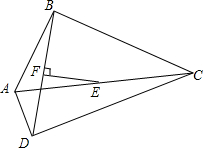 如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.
如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.