题目内容
16.进位数是一种记数方式,可以用有限的数字符号代表所有的数值,使用数字符号的数目称为基数,基数为n,即可称n进制,现在最常用的是十进制,通常使用10个阿拉伯数字0~9进行记数,特点是逢十进一,对于任意一个用n(n≤10)进制表示的数,通常使用n个阿拉伯数字0~(n-1)进行记数,特点是逢n进一,我们可以通过以下方式把它转化为十进制:例如:五进制数(234)5=2×52+3×5+4=69,记作(234)5=69,
七进制数(136)7=1×72+3×7+6=76,记作(136)7=76.
(1)请将以下两个数转化为十进制:(331)5=91,(46)7=34
(2)若一个正数可以用七进制表示为($\overline{abc}$)7,也可以用五进制表示为($\overline{cba}$)5,请求出这个数并用十进制表示.
分析 (1)根据进制的计算规则列式计算即可得;
(2)由题意得出72a+7b+c=52c+5b+a,即24a+b=12c,结合1≤a≤9,0≤b≤9,1≤c≤9,且a、b、c均为整数得出a、b、c的值,表示成十进制即可.
解答 解:(1)根据题意知,(331)5=3×52+3×5+1=91,(46)7=4×7+6=34,
故答案为:91,34;
(2)根据题意得:72a+7b+c=52c+5b+a,
整理得24a+b=12c,
∵1≤a≤9,0≤b≤9,1≤c≤9,且a、b、c均为整数,
∴a=1、b=0、c=2,此数用十进制表示为102;
a=2、b=0、c=4,此数用十进制表示为204;
a=3、b=0、c=6时,此数用十进制表示为306;
a=4、b=0、c=8时,此数用十进制表示为408.
点评 本题主要考查有理数的混合运算和进制计算规则,根据题意弄清进制的计算规则是解题的根本,由题意列出a、b、c的等式结合其范围得出具体数值是解题的关键.

练习册系列答案
相关题目
9.某汽车销售店计划上半年每月销售20辆汽车,由于某种原因未能按计划执行,实际每月的销售情况如下表(规定比计划月销售量增加为正,减少为负):
(1)请把上表补充完整;
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 实际月销售(辆) | 24 | 19 | 22 | 23 | ||
| 比计划月销售量增(辆) | +4 | -2 | 0 | +3 |
(2)销量最多的一个月比销量最少的一个月多销售多少辆?
(3)这半年内总销量比原计划多了还是少了?多或少了多少辆?
(4)这半年内实际平均每月销售了多少辆汽车?
4.小明和小亮玩扑克牌游戏,小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌都为a张,且a≥10;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出五张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
(1)填写下表中的空格:
(2)如若第四步完成后,左边一堆牌的张数恰好是右边一堆牌的张数的3倍,试求第一步后,每堆牌各有多少张?
第一步:分发左、中、右三堆牌,每堆牌都为a张,且a≥10;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出五张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
(1)填写下表中的空格:
| 步骤 | 左边一堆牌的张数 | 中间一堆牌的张数 | 右边一堆牌的张数 |
| 第一步后 | a | a | a |
| 第二步后 | a-2 | a+2 | a |
| 第三步后 | a-2 | a+7 | a-5 |
| 第四步后 | 2a-4 | 9 | a-5 |
 如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数.
如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC,垂足为F,AF交BD于E,若DE=2AB,求∠AED的度数. 如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.
如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD. 今年5月8日母亲节那天,某班很多同学给妈妈准备了鲜花和礼盒,根据图中的信息
今年5月8日母亲节那天,某班很多同学给妈妈准备了鲜花和礼盒,根据图中的信息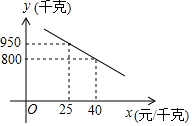 某商场经营一种海产品,进价是每千克20元,根据市场调查发现,每日的销售量y(千克)与售价x(元/千克)是一次函数关系,如图所示:
某商场经营一种海产品,进价是每千克20元,根据市场调查发现,每日的销售量y(千克)与售价x(元/千克)是一次函数关系,如图所示: