题目内容
14.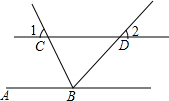 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数,下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数,下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).解:∵AB∥CD已知
∴∠ABC=∠1=65° (两直线平行,同位角相等)
∠ABD+∠BDC=180° (两直线平行,同旁内角互补)
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130° (角平分线定义)
∴∠BDC=180°-∠ABD=50°,
∴∠2=∠BDC=50°(对顶角相等).
分析 由两直线平行判断同位角相等和同旁内角互补,由角平分线的定义和对顶角相等,得到结论.
解答 解:∵AB∥CD,
∴∠ABC=∠1=65° ( 两直线平行,同位角相等)
∠ABD+∠BDC=180° ( 两直线平行,同旁内角互补)
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130° ( 角平分线定义)
∴∠BDC=180°-∠ABD=50°,
∴∠2=∠BDC=50°( 对顶角相等).
故答案为:∠ABC,两直线平行,同位角相等,两直线平行,同旁内角互补,角平分线定义,50°,对顶角相等.
点评 本题主要考查了平行线的性质问题,能够掌握并熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )
 如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{7}$ | D. | 3 |
2.二次函数y=x2-4x-5的图象的对称轴为( )
| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=2 | D. | 直线x=-2 |
19.下列计算错误的是( )
| A. | x2+x4=x6 | B. | 2xy+3xy=5xy | C. | (x3)2=x6 | D. | x6÷x3=x3 |
3.如果一个平行四边形的两条对角线相等,那么这个四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
 己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题:
己知如图,在直角坐标系中,矩形ABCD,点A(3,6),点B(5,6),点C(5,10),直线l:y=x以每秒1个单位的速度沿y轴向上运动,运动的时间为t秒.试解决下列问题: