题目内容
5. 如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )
如图,⊙O是△ABC的外接圆,⊙O的半径为2,sin∠B=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{7}$ | D. | 3 |
分析 作直径AD,连接CD,根据圆周角定理得到∠D=∠B,根据正弦的定义计算即可.
解答 解: 作直径AD,连接CD,
作直径AD,连接CD,
由圆周角定理得,∠D=∠B,
∵sin∠B=$\frac{3}{4}$,
∴sin∠D=$\frac{3}{4}$,即$\frac{AC}{AD}$=$\frac{3}{4}$,又AD=4,
∴AC=3,
故选:D.
点评 本题考查的是圆周角定理和锐角三角函数的定义,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.化简${(-\sqrt{5})^2}$的结果是( )
| A. | 25 | B. | -5 | C. | 5 | D. | ±5 |
10.下列运算结果是负数的是( )
| A. | (-3)×(-2) | B. | (-3)2÷3 | C. | |-3|÷6 | D. | -3-2×(+4) |
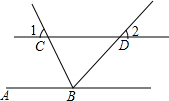 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数,下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数,下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).