题目内容
1. 如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
分析 先根据旋转的性质得∠ABD=∠CBE,∠E=∠ACB=70°,BC=BE,则根据等腰三角形的性质得∠BCE=∠E=70°,再利用三角形内角和计算出∠CBE,从而得到∠ABD的度数.
解答 解:∵△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),
∴∠ABD=∠CBE,∠E=∠ACB=70°,BC=BE,
∴∠BCE=∠E=70°,
∴∠CBE=180°-70°-70°=40°,
∴∠ABD=40°.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
13.若方程组$\left\{\begin{array}{l}{4x+3y=5}\\{kx+(1-k)y=8}\end{array}\right.$的解中,x的值比y的值的相反数大1,则k的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | 无答案 |
11.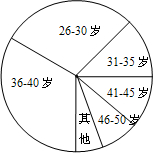 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
(1)请将统计表中遗漏的数据补上;
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?
 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?
 如图,△ABC的两条高AD、CE相交于点M,已知∠BAC=30°,∠ACB=75°,求∠AMC的度数.
如图,△ABC的两条高AD、CE相交于点M,已知∠BAC=30°,∠ACB=75°,求∠AMC的度数.

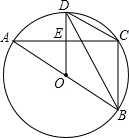 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD,CD.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD,CD.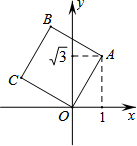 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).
如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,$\sqrt{3}$),则(1)OA的长为2,(2)点C的坐标为(-$\sqrt{3}$,1).