题目内容
6.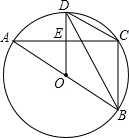 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD,CD.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD,CD.(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:四边形OBCD是菱形.
分析 (1)根据垂径定理得到$\widehat{AD}$=$\widehat{DC}$,根据等弧所对的圆周角相等证明结论;
(2)根据30°所对的直角边是斜边的一半得到BC=OD,得到平行四边形DOBC,根据半径相等和菱形的判定定理证明结论.
解答 (1)证明:∵OD⊥AC,
∴$\widehat{AD}$=$\widehat{DC}$,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,又OD⊥AC,
∴OD∥BC,
∵OB=OD,
∴∠OBD=∠ODB=30°,
∴∠AOD=60°,
∴∠A=30°,∴BC=$\frac{1}{2}$AB=OB,
∴BC=OD,又OD∥BC,
∴四边形DOBC是平行四边形,又OD∥BC,
∴四边形OBCD是菱形.
点评 吧考查的是三角形的外接圆和外心的性质以及菱形的判定,掌握直角所对的圆周角是直角、等弧所对的圆周角相等和菱形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
 如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )
如图,△ABC中,∠ACB=70°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
16. 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )| A. | 校 | B. | 东 | C. | 母 | D. | 中 |
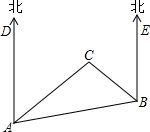 如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
如图,C岛在A岛的北偏东55°方向,B岛在A岛的北偏东85°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度? 如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.
如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.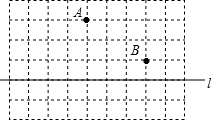 如图,是边长为1的小正方形组成的网格图,图中线与线的交点叫做格点.A、B都是格点,l是网格图中的一条直线.
如图,是边长为1的小正方形组成的网格图,图中线与线的交点叫做格点.A、B都是格点,l是网格图中的一条直线. 如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.
如图,在矩形ABCD中,AB=6cm,BC=10cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,当一个点到达终点时,另一个点立即停止移动,点P运动时间为t秒.