题目内容
5.学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,图是根据调查结果绘制的两幅不完整的统计图.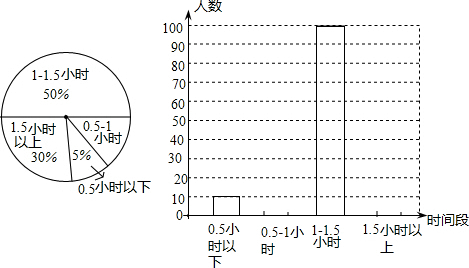
请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了200名学生;
(2)将条形统计图补充完整;
(3)平均每天参加体育活动的时间为“0.5~1小时”部分所对应扇形的圆心角是54度;
(4)若该校有3000名学生,请你估计全校有600名学生平均每天参加体育活动的时间不超1小时.
分析 (1)根据统计图中的数据可以求得本次调查的学生数;
(2)根据题意和统计图中的数据可以求得1.5小时以上和0.5~1小时的学生数,从而可以将统计图补充完整;
(3)根据题意和统计图中的数据可以计算出平均每天参加体育活动的时间为“0.5~1小时”部分所对应扇形的圆心角的度数;
(4)根据题意可以计算出全校有多少名学生平均每天参加体育活动的时间不超1小时.
解答 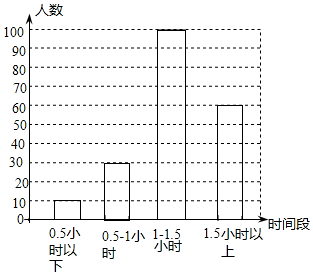 解:(1)由题意可得,
解:(1)由题意可得,
本次一共调查了:10÷5%=200(名),
故答案为:200;
(2)1.5小时以上的有:200×30%=60(名),
0.5~1小时的有:200-10-100-60=30(名),
补全的条形统计图如右图所示;
(3)平均每天参加体育活动的时间为“0.5~1小时”部分所对应扇形的圆心角是:360°×$\frac{30}{200}$=54°,
故答案为:54;
(4)∵3000×$\frac{10+30}{200}$=600,
∴全校有600名学生平均每天参加体育活动的时间不超1小时,
故答案为:600.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
16.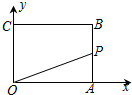 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. |  | D. | 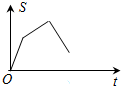 |
20.若函数y=$\frac{k-3}{x}$的图象在其所在的每一象限内,y随x的增大而增大,则k的取值范围是( )
| A. | k>3 | B. | k<3 | C. | k>-3 | D. | k<-3 |
10.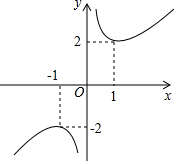 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )| A. | 该函数的图象是中心对称图形 | |
| B. | 当x>0时,该函数在x=1时取得最小值2 | |
| C. | 在每个象限内,y的值随x值的增大而减小 | |
| D. | y的值不可能为1 |
 形状相同,大小相等的两个小木块放置于桌面,则其主视图是( )
形状相同,大小相等的两个小木块放置于桌面,则其主视图是( )



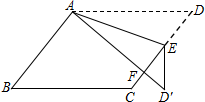 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.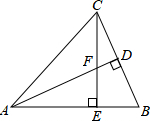 如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.
如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.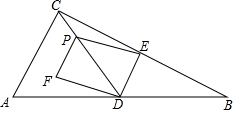 在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点.点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作平行四边形EDFP.设点P的运动时间为t(t≥0)(秒).
在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点.点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作平行四边形EDFP.设点P的运动时间为t(t≥0)(秒).