题目内容
13.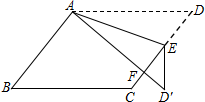 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
分析 由平行四边形的性质得出∠D=∠B=50°,由折叠的性质得:∠D′=∠D=50°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠AEF=70°,与三角形内角和定理求出∠AED′=110°,即可得出∠FED′的大小.
解答  解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=50°,
由折叠的性质得:∠D′=∠D=50°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=50°+20°=70°,∠AED′=180°-∠EAD′-∠D′=110°,
∴∠FED′=110°-70°=40°;
故答案为:40.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.

练习册系列答案
相关题目
8.市园林处为了对一段公路进行绿化,计划购买A,B两种风景树共900棵.A,B两种树的相关信息如表:
若购买A种树x棵,购树所需的总费用为y元.
(1)求y与x之间的函数关系式.
(2)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?此时最低费用为多少?
| 品种项目 | 单价(元/棵) | 成活率 |
| A | 80 | 92% |
| B | 100 | 98% |
(1)求y与x之间的函数关系式.
(2)若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?此时最低费用为多少?
18.数据7,-7,0,6,-6,7的中位数和众数分别是( )
| A. | 6,-6 | B. | 3,7 | C. | 0,6 | D. | 0,7 |
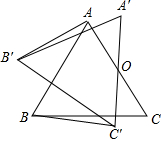 已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.
已知:如图,等边三角形△ABC,O为AC边的中点,将△ABC绕点O顺时针旋转α角(0°<α<90°)到△A′B′C′的位置,连接AB′,BC′.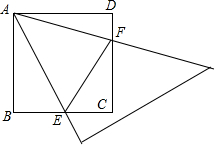 如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
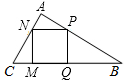 如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.
如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.