题目内容
14.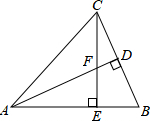 如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.
如图,△ABC中,AB=AC,AD⊥BC于D,CE⊥AB于E,AD交CE于F,AE=CE,求证:AF=2CD.
分析 首先证明DC=BD,再由△AEF≌△CEB,推出AF=BC即可解决问题.
解答 证明: ∵AB=AC,AD⊥BC,
∵AB=AC,AD⊥BC,
∴CD=BD,
∵CE⊥AB,
∴∠AEF=∠CEB=90°,
∵∠BCE+∠B=90°,∠EAF+∠B=90°,
∴∠BCE=∠EAF,
在△AEF和CEB中,
$\left\{\begin{array}{l}{∠EAF=∠ECB}\\{AE=EC}\\{∠AEF=∠CEB}\end{array}\right.$,
∴△AEF≌△CEB,
∴AF=BC=2CD,
即AF=2CD.
点评 本题考查等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.下列四个手机APP图标中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
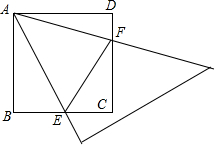 如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
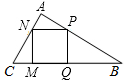 如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.
如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形. 如图,△ABC中,∠C=50°,∠B=25°,AD是角平分线,点E在AB上,AE=AC.
如图,△ABC中,∠C=50°,∠B=25°,AD是角平分线,点E在AB上,AE=AC.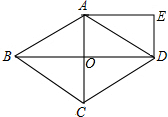 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长.