��Ŀ����
15��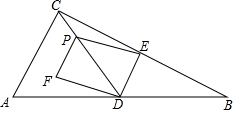 �ڡ�ABC�У���ACB=90�㣬AC=2$\sqrt{5}$��BC=4$\sqrt{5}$��D��E�ֱ��DZ�AB��BC���е㣮��P�ӵ�C���������߶�CD������ÿ��1����λ���ȵ��ٶ��˶�������P���D���غ�ʱ����EP��EDΪ�ڱ���ƽ���ı���EDFP�����P���˶�ʱ��Ϊt��t��0�����룩��
�ڡ�ABC�У���ACB=90�㣬AC=2$\sqrt{5}$��BC=4$\sqrt{5}$��D��E�ֱ��DZ�AB��BC���е㣮��P�ӵ�C���������߶�CD������ÿ��1����λ���ȵ��ٶ��˶�������P���D���غ�ʱ����EP��EDΪ�ڱ���ƽ���ı���EDFP�����P���˶�ʱ��Ϊt��t��0�����룩����1���߶�AB�ij�Ϊ10��
��2������DPF=��PFDʱ����t��ֵ��
��3������P���߶�CD��ʱ����ƽ���ı���EDFP���ABC�ص�����ͼ�ε����Ϊy��ƽ����λ������y��t֮��ĺ�����ϵʽ��
��4������AF������AFD��������PDE��������ʱ��ֱ��д��t��ֵ��
���� ��1�����ù��ɶ����ó�AB�ij���
��2����ͼ1��֤��PE��DB����CE=EB��������λ�ߵ����ۿɵã�PC=PD=$\frac{5}{2}$����t=$\frac{5}{2}$��
��3�������������
�ٵ�0��t��$\frac{5}{2}$ʱ����ͼ2��ƽ���ı���EDFP���ABC�ص�����ͼ�ε����Ϊƽ���ı���EDFP���������PM��DE�ڵ�M������ƽ���ı��ε������ʽ�ɵý��ۣ�
�ڵ�$\frac{5}{2}$��t��5ʱ����ͼ3��ͬ����PH=$\frac{2\sqrt{5}}{5}$��5-t��������y=S��PHD+S��PDE����ɵù�ϵʽ��
��4���ٵ�t=0ʱ����AFD��������PDE�������ȣ�
����ͼ4����A��P��E���㹲��ʱ�����ݵȵȸߵ�������������ȵã���AFD��������PDE�������ȣ����������ε���λ�ߵó�t��ֵ��
��� 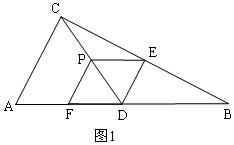 �⣺��1����ABC�У�
�⣺��1����ABC�У�
�ߡ�ACB=90�㣬AC=2$\sqrt{5}$��BC=4$\sqrt{5}$��
��AB=$\sqrt{��2\sqrt{5}��^{2}+��4\sqrt{5}��^{2}}$=10��
�ʴ�Ϊ��10��
��2����ͼ1�У����ı���ABCD��ƽ���ı��Σ�
��FP��DE��PE��DF��
���DPF=��PDE��
�ߡ�ACB=90�㣬AD=DB��
��CD=DB=DA=5��
��CE=EB��
��DE��BC����CDE=��EDB��
�ߡ�DPF=��PFD��
���PED=��BDE��
��PE��DB��
��CE=EB��
��PC=PD=$\frac{5}{2}$��
��t=$\frac{5}{2}$��
��3���ٵ�0��t��$\frac{5}{2}$ʱ����ͼ2����PM��DE�ڵ�M��
������ã�PC=t����DP=5-t��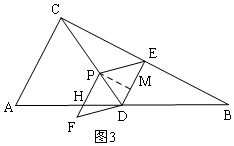
��PM��CE��
��$\frac{PM}{CE}=\frac{DP}{DC}$��
��$\frac{PM}{2\sqrt{5}}$=$\frac{5-t}{5}$��
��PM=$\frac{2\sqrt{5}}{5}$��5-t����
��y=DE•PM=$\sqrt{5}$$•\frac{2\sqrt{5}}{5}��5-t��$=-2t+10��
�ڵ�$\frac{5}{2}$��t��5ʱ����ͼ3��
��PH��AC��
��$\frac{PH}{AC}=\frac{DP}{CD}$��
��$\frac{PH}{2\sqrt{5}}=\frac{5-t}{5}$��
��PH=$\frac{2\sqrt{5}}{5}$��5-t����
��y=S��PHD+S��PDE=$\frac{1}{2}$PH•PM+$\frac{1}{2}$��-2t+10��=$\frac{1}{2}$•$\frac{2\sqrt{5}}{5}$��5-t��•$\frac{2\sqrt{5}}{5}$��5-t��-t+5=$\frac{2}{5}{t}^{2}$-5t+15��
����������y=$\left\{\begin{array}{l}{-2t+10��0��t��\frac{5}{2}��}\\{\frac{2}{5}{t}^{2}-5t+15��\frac{5}{2}��t��5��}\end{array}\right.$��
��4���ٵ�t=0ʱ����AFD��������PDE�������ȣ�
����ͼ4����A��P��E���㹲��ʱ��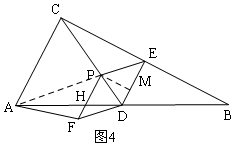
��AE��DF��
��S��ADF=S��PDF=S��PED��
��DE��AC��
��$\frac{DE}{AC}=\frac{PD}{PC}=\frac{1}{2}$��
��PC=$\frac{2}{3}$CD=$\frac{10}{3}$��
��t=$\frac{10}{3}$��
�൱t=0��t=$\frac{10}{3}$ʱ����AFD��������PDE�������ȣ�
���� �������ı��ε��ۺ��⣬�����������ε���λ�߶�����ƽ���ı��ε����ʡ�ƽ���߷��߶γɱ��������������˶����⼰�ص�����ͼ�ε�������⣬���Ѷȣ���������˷������۵�˼�룬�ڼ����ص�����ͼ��ʱ���������ν�Ͻ�����⣬���ڵ����ʣ��������յȵȸߵ���������������ǹؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | ��x1��x2��3x2+4x-5=0����������x1+x2=-$\frac{5}{3}$�� | |
| B�� | ����ʽ-$\frac{4{x}^{2}{y}^{2}}{7}$��ϵ����-4 | |
| C�� | ��|x-1|+��y-3��2=0����x=1��y=3 | |
| D�� | ����ʽ����$\frac{x}{x-3}$-2=$\frac{{m}^{2}}{x-3}$����������m=3�� |
| A�� | ��-a��2•a2=-a4 | B�� | ��-x-2y����x+2y��=x2-4y2 | ||
| C�� | ��-3x3y��2=9x9y2 | D�� | 2x2y+3yx2=5x2y |
| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 2.026��1010Ԫ | B�� | 2.026��109Ԫ | C�� | 2.026��108Ԫ | D�� | 2.026��1011Ԫ |