题目内容
20.若点A(-3,m)在正比例函数y=-$\frac{4}{3}$x的图象上,则点A到坐标原点的距离为( )| A. | 7 | B. | 5 | C. | 4 | D. | 3 |
分析 直接把点A(-3,m)代入正比例函数y=-$\frac{4}{3}$x,求出m的值,然后根据勾股定理即可求得.
解答 解:∵点A(-3,m)在正比例函数y=-$\frac{4}{3}$x的图象上,
∴m=(-$\frac{4}{3}$)×(-3)=4,
∴A(-3,4)
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
11.节约是一种美德,节约是一种智慧,据不完全统计,全国每年浪费的食物若折合成粮食可养活约360000000人,把350000000用科学记数法可以表示为( )
| A. | 3.5×1010 | B. | 3.5×109 | C. | 3.5×108 | D. | 3.5×107 |
8.十边形的内角和为( )
| A. | 1800° | B. | 1620° | C. | 1440° | D. | 1260° |
15.若一个正比例函数的图象经过点(-2,1),则这个图象也一定经过点( )
| A. | (-$\frac{1}{2}$,1) | B. | (2,-1) | C. | (-1,2) | D. | (1,$\frac{1}{2}$) |
12.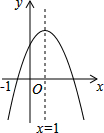 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )
①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
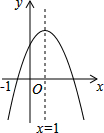 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
9.对于数据:1,7,5,5,3,4,3.下列说法中错误的是( )
| A. | 这组数据的平均数是4 | B. | 这组数据的众数是5和3 | ||
| C. | 这组数据的中位数是4 | D. | 这组数据的方差是22 |
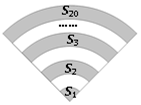 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=195π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=195π.