题目内容
12.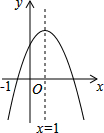 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据图象知x=1和x=-1时的函数值可判断①②;根据开口方向和对称轴可判断③④,由抛物线与y轴的交点可判断⑤.
解答 解:由图象可知,当x=1时,y=a+b+c>0,故①正确;
当x=-1时,y=a-b+c<0,故②正确;
∵抛物线开口朝下,
∴a<0,
∵对称轴x=-$\frac{b}{2a}$=1,
∴b>0,b=-2a,故③正确,④错误;
∵当x=0时,y=c>0,
∴abc<0,故⑤正确,
故选:B.
点评 本题考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
2.2017年4月20日19时41分,中国自主研制的首个货运飞船“天舟一号”,搭载“长征七号”火箭在海南省文昌航天发射场发射成功,被称为“太空快递小哥”的“天舟一号”,起飞重量约13吨,将13吨用科学记数法可表示为( )
| A. | 13×103千克 | B. | 1.3×103千克 | C. | 1.3×104千克 | D. | 1.3×105千克 |
17.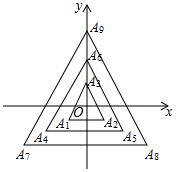 如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )
如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )
 如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )
如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )| A. | (0,448) | B. | (-672,$224\sqrt{3}$) | C. | (0,$448\sqrt{3}$) | D. | (0,$224\sqrt{3}$) |
4.如果$\sqrt{{a}^{2}}$=-a,则关于x的一元二次方程:2x2-x+a=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 根的情况不确定 |
1.下列单项式中,与ab2是同类项的是( )
| A. | 2ab | B. | 3ab2 | C. | 4a2b | D. | 5a2b2 |
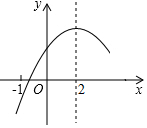 二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
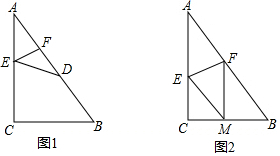
二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )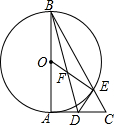 如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F