题目内容
15.若一个正比例函数的图象经过点(-2,1),则这个图象也一定经过点( )| A. | (-$\frac{1}{2}$,1) | B. | (2,-1) | C. | (-1,2) | D. | (1,$\frac{1}{2}$) |
分析 利用一次函数图象上点的坐标特征,将点(-2,1)代入y=kx求得k值,求出函数解析式,然后再判断点是否在函数图象上.
解答 解:∵正比例函数y=kx经过点(-2,1),
∴1=-2k,
解得k=-$\frac{1}{2}$;
∴正比例函数的解析式是y=-$\frac{1}{2}$x;
A、∵当x=-$\frac{1}{2}$时,y≠1,∴点(-$\frac{1}{2}$,1)不在该函数图象上;故本选项错误;
B、∵当x=2时,y=-1,∴点(2,-1)在该函数图象上;故本选项正确;
C、∵当x=-1时,y≠2,∴点(-1,2)不在该函数图象上;故本选项错误;
D、∵当x=1时,y≠$\frac{1}{2}$,∴点(1,$\frac{1}{2}$)不在该函数图象上;故本选项错误.
故选B.
点评 本题主要考查了一次函数图象上的点的坐标特征.解答此题时,利用正比例函数y=kx中的k是定值来确定函数的图象一定的点.

练习册系列答案
相关题目
5.王红在做一道双选择题(即有两个选项是正确的)时,发现四个选项都有可能正确,于是她从中任选两个,那么她做对此题的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
10.1不是-1的( )
| A. | 相反数 | B. | 绝对值 | C. | 平方数 | D. | 倒数 |
4.如果$\sqrt{{a}^{2}}$=-a,则关于x的一元二次方程:2x2-x+a=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 根的情况不确定 |
5.若a<$\sqrt{10}$-1<b,且a,b是两个连续的整数,则a-b的值是( )
| A. | 9 | B. | 8 | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
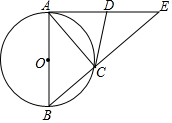 已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.
已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.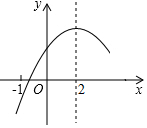 二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(-1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )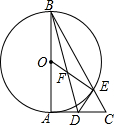 如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F