题目内容
6. 某中学食堂提供了四种价格的午餐供学生选择,这四种价格分别是:A.3元,B.4元,C.5元,D.6元.为了解学生对四种午餐的购买情况,学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况,依据统计数据制成如下的统计图表:
某中学食堂提供了四种价格的午餐供学生选择,这四种价格分别是:A.3元,B.4元,C.5元,D.6元.为了解学生对四种午餐的购买情况,学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况,依据统计数据制成如下的统计图表:甲、乙两班学生购买四种午餐情况统计表
| A | B | C | D | |
| 甲 | 6 | 22 | 16 | 6 |
| 乙 | ? | 13 | 25 | 3 |
(2)从这次接受调查的学生中随机抽查一人,恰好是购买C种午餐的学生的概率是41%;
(3)请从平均数、中位数和众数的角度分析甲、乙两个班学生购买的午餐价格高低情况.
分析 (1)由乙班学生购买C午餐的人数为25人,占百分比为:50%,即可求得乙班学生人数;
(2)用购买C种午餐的学生数除以总人数即可求解;
(3)根据平均数、中位数和众数定义,分别求出甲、乙两个班学生购买午餐费用的平均数、中位数和众数,即可求得答案.
解答 解:(1)∵乙班学生购买C午餐的人数为25人,占百分比为:50%,
∴乙班学生人数为:25÷50%=50(人).
故答案为50;
(2)∵甲班学生人数为:6+22+16+6=50(人),
乙班学生人数共50人,
∴从这次接受调查的学生中随机抽查一人,恰好是购买C种午餐的学生的概率是$\frac{16+25}{50+50}$=41%.
故答案为41%;
(3)∵甲班购买午餐费用的平均数为:(6×3+22×4+16×5+6×6)÷50=4.44(元),
乙班购买午餐费用的平均数为:(9×3+13×4+25×5+3×6)÷50=4.44(元);
甲班购买午餐费用的中位数是:购买B午餐:4元;乙班购买午餐费用的中位数是:购买C午餐:5元;
甲班购买午餐费用的众数是:购买B午餐:4元;乙班购买午餐费用的众数是:购买C午餐:5元;
∴乙班购买的午餐价格较高.
点评 本题考查扇形统计图、平均数、众数、中位数以及概率公式.注意在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比.

练习册系列答案
相关题目
1. 如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
 如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )| A. | (2,4) | B. | (2,3) | C. | (3,3) | D. | (3,4) |
15.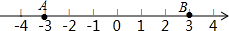 如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
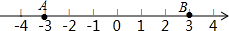 如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,将△ABC第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1、B1、C1,得到△A1B1C1,第二次操作:分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2、B2、C2,得到△A2B2C2…按此规律,若△A3B3C3的面积是686,则△ABC的面积为2.
如图,将△ABC第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1、B1、C1,得到△A1B1C1,第二次操作:分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2、B2、C2,得到△A2B2C2…按此规律,若△A3B3C3的面积是686,则△ABC的面积为2. 如图,△ABC中,DE∥BC,EF∥AB,AD=3,AB=7,BC=6,则FC的长为$\frac{24}{7}$.
如图,△ABC中,DE∥BC,EF∥AB,AD=3,AB=7,BC=6,则FC的长为$\frac{24}{7}$. 如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=5,BC=6,则sinC=$\frac{4}{5}$.
如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=5,BC=6,则sinC=$\frac{4}{5}$. 如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2).
如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2).