题目内容
15．
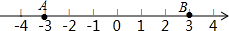如图，数轴上两点A、B在线段AB上任意取一点C，则点C到表示1的距离不大于2的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
分析 先求出AB两点间的距离，根据距离的定义找出符合条件的点，再根据概率公式即可得出答案．
解答 解：∵AB间距离为6，点C到表示1的点的距离不大于2的点是-1到3之间的点，满足条件的点组成的线段的长是4．
∴点C到表示1的距离不大于2的概率为$\frac{4}{6}$=$\frac{2}{3}$；
故选D．
点评 本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
练习册系列答案
相关题目
6．
某中学食堂提供了四种价格的午餐供学生选择，这四种价格分别是：A．3元，B．4元，C．5元，D．6元．为了解学生对四种午餐的购买情况，学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况，依据统计数据制成如下的统计图表：
甲、乙两班学生购买四种午餐情况统计表
（1）乙班有学生50人；
（2）从这次接受调查的学生中随机抽查一人，恰好是购买C种午餐的学生的概率是41%；
（3）请从平均数、中位数和众数的角度分析甲、乙两个班学生购买的午餐价格高低情况．
某中学食堂提供了四种价格的午餐供学生选择，这四种价格分别是：A．3元，B．4元，C．5元，D．6元．为了解学生对四种午餐的购买情况，学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况，依据统计数据制成如下的统计图表：甲、乙两班学生购买四种午餐情况统计表
| A | B | C | D | |
| 甲 | 6 | 22 | 16 | 6 |
| 乙 | ？ | 13 | 25 | 3 |
（2）从这次接受调查的学生中随机抽查一人，恰好是购买C种午餐的学生的概率是41%；
（3）请从平均数、中位数和众数的角度分析甲、乙两个班学生购买的午餐价格高低情况．
10．在直角△ABC，∠C=90°，sinA=$\frac{3}{5}$，BC=8，则AB的长为（ ）
| A． | 10 | B． | $\frac{40}{3}$ | C． | $\frac{24}{5}$ | D． | 12 |
20．若火箭点火发射之后5秒记为+5秒，那么火箭点火发射之前10秒应记为（ ）秒．
| A． | +10 | B． | -10 | C． | $+\frac{1}{10}$ | D． | $-\frac{1}{10}$ |
7．
如图，在△ABC中，点D、E分别在BC、AB边上，DF∥AB，交AC边于点H，EF∥BC，交AC边于点G，则下列结论中正确的是（ ）
如图，在△ABC中，点D、E分别在BC、AB边上，DF∥AB，交AC边于点H，EF∥BC，交AC边于点G，则下列结论中正确的是（ ）| A． | $\frac{AE}{BE}=\frac{AG}{CG}$ | B． | $\frac{EG}{GF}=\frac{AG}{CH}$ | C． | $\frac{CH}{CF}=\frac{CD}{BD}$ | D． | $\frac{EF}{CD}=\frac{AG}{CH}$ |
4．
如图，在圆心角为90°的扇形OAB中，半径OA=4cm，C为弧AB的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为（ ）cm2．
如图，在圆心角为90°的扇形OAB中，半径OA=4cm，C为弧AB的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为（ ）cm2．| A． | 4π-2$\sqrt{2}$-2 | B． | 4π-2 | C． | 2π+2$\sqrt{2}$-2 | D． | 2π+2$\sqrt{2}$ |
