题目内容
16.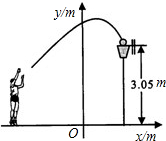 一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.
一位篮球运动员投篮,球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行,然后准确落入篮筐内,已知篮筐的中心距离底面的距离为3.05m.(1)求球在空中运行的最大高度为多少m?
(2)如果该运动员跳投时,球出手离地面的高度为2.25m,要想投入篮筐,则问他距离蓝筐中心的水平距离是多少?
分析 (1)由抛物线的顶点坐标即可得;
(2)分别求出y=3.05和y=2.25时x的值即可得出答案.
解答 解:(1)∵y=-$\frac{1}{5}$x2+$\frac{7}{2}$的顶点坐标为(0,$\frac{7}{2}$),
∴球在空中运行的最大高度为$\frac{7}{2}$m;
(2)当y=3.05时,-0.2x2+3.5=3.05,
解得:x=±1.5,
∵x>0,
∴x=1.5;
当y=2.25时,-0.2x2+3.5=2.25,
解得:x=2.5或x=-2.5,
由1.5+2.5=4(m),
故他距离蓝筐中心的水平距离是4米.
点评 本题主要考查二次函数的应用,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
7.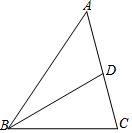 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
 如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )
如图,线段BD为锐角△ABC上AC边上的中线,E为△ABC的边上的一个动点,则使△BDE为直角三角形的点E的位置有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11.下列说法错误的是( )
| A. |  直线l经过点A | B. |  直线a,b相交于点A | ||
| C. |  点C在线段AB上 | D. |  射线CD与线段AB有公共点 |
 如图,已知AB⊥BC,EF⊥BC,CD⊥AD.
如图,已知AB⊥BC,EF⊥BC,CD⊥AD.  请阅读下列材料,并完成相应的任务:
请阅读下列材料,并完成相应的任务: