题目内容
13．若关于x的多项式3x2+mx+n因式分解的结果为3（x+2）（x-1），求m、n的值．分析 因式分解结果利用多项式乘以多项式法则计算，再利用多项式相等的条件求出m与n的值即可．
解答 解：根据题意得：3x2+mx+n=3（x+2）（x-1）=3x2+3x-6，
可得m=3，n=-6．
点评 此题考查了因式分解-十字相乘法，熟练掌握十字相乘的方法是解本题的关键．
练习册系列答案
相关题目
3．使代数式$\frac{2x}{x-2}$有意义的x的取值范围为（ ）
| A． | x＞2 | B． | x≠0 | C． | x＜2 | D． | x≠2 |
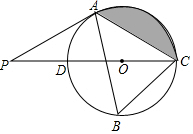如图，在⊙O的内接三角形ABC中，∠ABC=60°，AC=5，过点A作⊙O的切线交直径CD的延长线于点P．
1．抛物线y=2（x+3）2-2的顶点坐标是（ ）
| A． | （-3，2） | B． | （3，2） | C． | （3，-2） | D． | （-3，-2） |
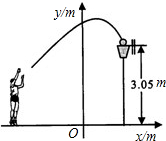一位篮球运动员投篮，球沿抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$运行，然后准确落入篮筐内，已知篮筐的中心距离底面的距离为3.05m．