题目内容
6.已知二次函数y=-x2-2x+3.(1)求它的顶点坐标和对称轴;
(2)求它与x轴、y轴的交点坐标;
(3)直接写出x为何值时,y≤0?
分析 (1)将抛物线的一般式化为顶点式,就可以确定对称轴,顶点;
(2)要求抛物线与x轴的交点,就要把解析式化为交点式,即可得到与坐标轴交点的坐标,令x=0求得与y轴的交点坐标;
(3)利用二次函数的性质与x轴的交点坐标直接得出答案即可.
解答 解:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点(1,4),对称轴x=1;
(2)∵y=-x2+2x+3=-(x-3)(x+1)
∴与x轴交点(3,0),(-1,0),与y轴交点(0,3);
(2)当x≥3,或x≤-1时,y≤0.
点评 此题考查二次函数的性质,抛物线的对称轴、顶点坐标与抛物线解析式的关系,抛物线的顶点式:y=a(x-h)2+k,顶点坐标为(h,k),对称轴x=h.同时考查了用抛物线与x轴的交点坐标.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
3.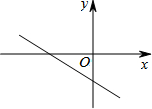 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )| A. | a>0 | B. | -3<a<0 | C. | a<-3 | D. | a<0 |
14.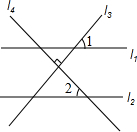 如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
 如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )
如图,直线l1∥l2,l3⊥l4,∠1=46°,那么∠2的度数为( )| A. | 46° | B. | 44° | C. | 23° | D. | 22° |
11.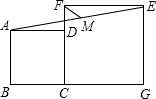 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
 如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )
如图,正方形ABCD,正方形CGEF的边长分别为4、6,且点B、C、G在同一条直线上,点M是线段AE的中点,连接MF,则MF的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
18.不等式(2x+1)(x-2)>3x2-x(x+2)的解集是( )
| A. | x<2 | B. | x<-2 | C. | x>-2 | D. | x>2 |