题目内容
3.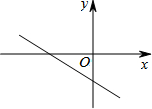 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a的取值范围是( )| A. | a>0 | B. | -3<a<0 | C. | a<-3 | D. | a<0 |
分析 首先求出方程组$\left\{\begin{array}{l}{y=-\frac{2}{3}x-3}\\{y=a}\end{array}\right.$的解,然后根据第四象限内点的坐标特征,列出关于a的不等式组,从而得出a的取值范围.
解答 解:解方程组$\left\{\begin{array}{l}{y=-\frac{2}{3}x-3}\\{y=a}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=\frac{-3(a+3)}{2}}\\{y=a}\end{array}\right.$.
∵交点在第四象限,
∴$\left\{\begin{array}{l}{\frac{-3(a+3)}{2}≥0}\\{a<0}\end{array}\right.$,
解得a<-3.
故选C.
点评 本题主要考查了一次函数与方程组的关系及第二象限内点的坐标特征.两个一次函数图象的交点坐标就是对应的二元一次方程组的解,反之,二元一次方程组的解就是对应的两个一次函数图象的交点坐标.第四象限内点的坐标特征:横坐标大于0,纵坐标小于0.

练习册系列答案
相关题目
13.能与4cm,9cm长的两根木棒首尾相接,钉成一个三角形的木棒是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
14.已知0.8622=0.7396,若x2=0.7396,则x的值等于( )
| A. | 0.862 | B. | -0.862 | C. | ±0.862 | D. | ±8.62 |
15.以下列各组数为边长,能构成直角三角形的是( )
| A. | 12,15,20 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 0.3,0.4,0.5 | D. | 32,42,52 |
12.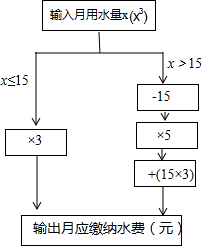 聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
(1)根据该程序转换机计算下列各户月应缴纳水费(元).
(2)当x>15时,月应缴纳水费(元)用x的代数式表示为5x-30;
(3)小丽家缴纳水费150元,则小丽家该月用水多少m3?
 聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
聪明的小明根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:(1)根据该程序转换机计算下列各户月应缴纳水费(元).
| 用户 | 张大爷 | 刘奶奶 | 王阿姨 | 小明家 |
| 输入(m3) | 8 | 15 | 18 | 25 |
| 输出(元) | 24 | 45 | 60 | 95 |
(3)小丽家缴纳水费150元,则小丽家该月用水多少m3?
 如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.
如图,AD垂直平分BC,连接AB,∠ABC的平分线交AD于点O,连结OC,若∠AOC=116°,则∠ABC的度数为52°.
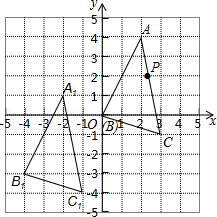 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2.