题目内容
10.(1)如图1,在边长为a的正方形中,画出两个长方形阴影,则阴影部分的面积是a2-b2(写成两数平方差的形式);(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是a+b,宽是a-b,面积是(a+b)(a-b)(写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式a2-b2=(a+b)(a-b)(用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n-p)(2m-n+p)
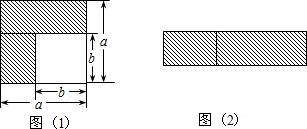
分析 (1)第一个图形中阴影部分的面积计算方法是边长是a的正方形的面积减去边长是b的小正方形的面积,等于a2-b2;
(2)第二个图形阴影部分是一个长是(a+b),宽是(a-b)的长方形,面积是(a+b)(a-b);
(3)根据这两个图形的阴影部分的面积相等即可得到结论;
(4)根据平方差公式即可得到结论.
解答  解:(1)∵大正方形的面积=a2,小正方形的面积=b2,
解:(1)∵大正方形的面积=a2,小正方形的面积=b2,
∴阴影部分的面积为:a2-b2,
故答案为:a2-b2;
(2)将阴影部分裁剪下来,重新拼成一个长方形,它的长是a+b,宽是a-b,面积是(a+b)(a-b);
故答案为:a+b,a-b,(a+b)(a-b);
(3)因而得到乘法公式是a2-b2=(a+b)(a-b);
故答案为:a2-b2=(a+b)(a-b);
(4)①10.3×9.7=(10+0.3)(10-0.3)=100-0.09=99.91;
②(2m+n-p)(2m-n+p)=[2m+(n-p)][2m-(n-p)]=(2m)2-(n-p)2=4m2-n2+2np-p2.
点评 本题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.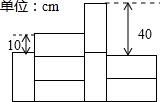 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
 如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )
如图是由同一种长方形的墙砖粘贴的部分墙面,其中3块横放的墙砖比1块竖放的墙砖高10cm,2块横放的墙砖比2块竖放的墙砖低40cm,则每块墙砖的面积是( )| A. | 425cm2 | B. | 525cm2 | C. | 600cm2 | D. | 800cm2 |
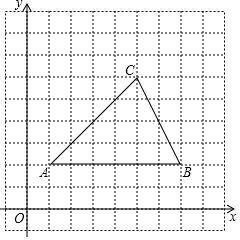 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(1,2),B(7,2),C(5,6).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(1,2),B(7,2),C(5,6).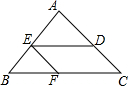 如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长.
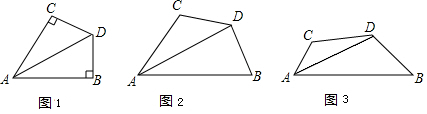
如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm,将线段DC沿着CB的方向平移7cm得到线段EF,点E、F分别落在边AB,BC上,求△EBF的周长.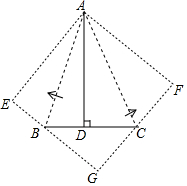 如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=3,AD=8,求DC的长.
如图,△ABC中,∠BAC=45°,AD⊥BC于D,BD=3,AD=8,求DC的长.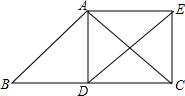 如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.
如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.