题目内容
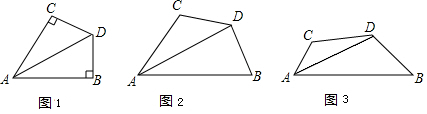
17.【感知】如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,求证:DB=DC.【探究】如图2,AD平分∠BAC,∠B+∠C=180°,∠B<90°,求证:DB=DC.
【应用】如图3,四边形ABCD中,∠ABD+∠ACD=180°,DB=DC,求证:AD平分∠BAC.
分析 【感知】根据角平分线的性质,欲证明DB=DC,只要证明DC⊥AC,DB⊥AB即可;
【探究】作DN⊥AC于N,DM⊥AB于M,欲证明DB=DC,只要证明△DNC≌△BMD即可;
【应用】作DN⊥AC于N,DM⊥AB于M,证得△DNC≌△BMD,得到DM=DN,根据角平分线的判定即的结论.
解答 证明:【感知】∵∠B+∠C=180°,∠B=90°,
∴DC⊥AC,DB⊥AB,
∵AD平分∠BAC,
∴DB=DC;
【探究】过点D作DN⊥AC于N,DM⊥AB于M,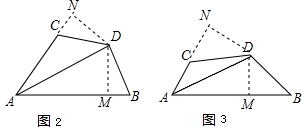
∵AD平分∠BAC,DN⊥AC,DM⊥AB,
∴DM=DN,
∵∠B+∠C=180°,∠NCD+∠ACD=180°,
∴∠B=∠NCD,
在△DNC和△BMD中,$\left\{\begin{array}{l}{∠B=∠NCD}\\{∠DNC=∠DMB=90°}\\{DM=DN}\end{array}\right.$,
∴△DNC≌△BMD,
∴DC=DB;
【应用】过点D作DN⊥AC于N,DM⊥AB于M,
∵∠ABD+∠ACD=180°,∠NCD+∠ACD=180°,
∴∠ABD=∠NCD,
在△DNC和△BMD中,
$\left\{\begin{array}{l}{∠ABD=∠NCD}\\{∠DNC=∠DMB=90°}\\{DB=DC}\end{array}\right.$,
∴△DNC≌△BMD,
∴DM=DN,
∵DN⊥AC,DM⊥AB,
∴AD平分∠BAC.
点评 本题考查全等三角形的判定和性质、角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
2.下列结论中,不正确的是( )
| A. | 两点之间的连线中,线段最短 | |
| B. | 两点确定一条直线 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 等角的余角相等 |
9.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | 2-x>2-y | C. | x+2>y+1 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |