题目内容
19.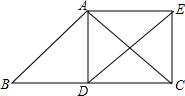 如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.
如图,在△ABC中,AB=AC,点D为边BC的中点,以AB、BD为邻边作?ABDE,连结AD、EC.(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?(直接写出满足的条件即可)
分析 (1)先根据等腰三角形三线合一的性质证明∠ADC=90°,再根据有一组对边平行且相等证明四边形ADCE是平行四边形,所以四边形ADCE是矩形;
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
解答 证明:(1)∵在△ABC中,AB=AC,点D为边BC的中点,
∴BD=DC,∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD且AE=BD,
∴AE∥DC且AE=DC,
∴四边形ADCE是平行四边形,
又∠ADC=90°,
∴四边形ADCE是矩形;
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形;
理由是:∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠ACD=45°,
∵∠ADC=90°,
∴△ADC是等腰直角三角形,
∴AD=CD,
∴矩形ADCE是正方形.
点评 本题考查了平行四边形、矩形、正方形的性质和判定、等腰直角三角形的性质和判定、等腰三角形三线合一的性质,熟练掌握矩形和正方形的判定是关键.

练习册系列答案
相关题目
7.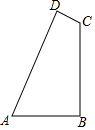 如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )
如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )
 如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )
如图,在四边形ABCD中,AB=3,BC=4,CD=1,AD=2$\sqrt{6}$,AB⊥BC,四边形ABCD的面积为( )| A. | 12 | B. | 6+$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{6}$+6 |
8.某中学开展“好书伴我成长”读书活动中,为了解七年级500名学生读书情况,随机调查了七年级50名学生读书的册数,统计图表如下图所示:
(1)这50个样本数据的众数为3,中位数是2.
(2)求这50个样本数据的平均数;
(3)根据样本数据,估计该校七年级500名学生在本次活动中读书多于2册的人数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
(2)求这50个样本数据的平均数;
(3)根据样本数据,估计该校七年级500名学生在本次活动中读书多于2册的人数.
9. 某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
(1)填空并把频数分布直方图补充完整:表中a的值为12;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:
某校举办首届“中国诗词大会”,经选拔后有50名学生参加决赛,每名学生限时默写50首古诗词,每正确默写一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表,请结合图表完成下列各题:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?

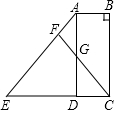 如图,矩形ABCD,E为射线CD上一点,连接AE,F为AE上一点,FC交AD于点G,FA=FG.求证:FE=FC.
如图,矩形ABCD,E为射线CD上一点,连接AE,F为AE上一点,FC交AD于点G,FA=FG.求证:FE=FC.