题目内容
已知点A(-1,m)、B(n,2)都在反比例函数y=-
的图象上,点C在y轴上,且∠ACB=90°,则点C的坐标为 .
| 6 |
| x |
考点:反比例函数图象上点的坐标特征
专题:
分析:把A、B的坐标分别代入反比例函数的解析式即可求得m、n的值,设C(0,b),根据勾股定理得出1+(6-b)2+32+(2-b)2=20,解方程即可求得C的坐标.
解答:解:∵点A(-1,m)、B(n,2)都在反比例函数y=-
的图象上,
把A(-1,m)代入得,m=-
=6,
∴A(-1,6),
把B(n,2)代入得,2=-
,解得n=-3,
∴B(-3,2),
设C(0,b),
∴AB2=(-1+3)2+(6-2)2=20,AC2=(-1)2+(6-b)2=1+(6-b)2,BC2=(-3)2+(2-b)2,
∵∠ACB=90°,
∴AC2+BC2=AB2,即1+(6-b)2+32+(2-b)2=20,
解得,b=3或b=5,
∴C的坐标为(0,3)或(0,5);
故答案为:(0,3)或(0,5);
| 6 |
| x |
把A(-1,m)代入得,m=-
| 6 |
| -1 |
∴A(-1,6),
把B(n,2)代入得,2=-
| 6 |
| n |
∴B(-3,2),
设C(0,b),
∴AB2=(-1+3)2+(6-2)2=20,AC2=(-1)2+(6-b)2=1+(6-b)2,BC2=(-3)2+(2-b)2,
∵∠ACB=90°,
∴AC2+BC2=AB2,即1+(6-b)2+32+(2-b)2=20,
解得,b=3或b=5,
∴C的坐标为(0,3)或(0,5);
故答案为:(0,3)或(0,5);
点评:本题考查了反比例函数图象上点的坐标特征以及勾股定理的应用,应用勾股定理是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
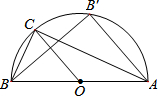 如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c>
如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c> 如图,是一座建筑纪念物的底座,小明想测量在地面上形成的∠AOB的度数,但一时没有办法,你能帮助他吗?动动你的脑筋.
如图,是一座建筑纪念物的底座,小明想测量在地面上形成的∠AOB的度数,但一时没有办法,你能帮助他吗?动动你的脑筋. 如图,在⊙O中,AB,CD是直径.
如图,在⊙O中,AB,CD是直径.
 如图,在Rt△ABC中,AB=10,sinA=0.6,把Rt△ABC绕着直线AC旋转一周,求所得圆锥的侧面展开图的弧长、圆心角、面积.
如图,在Rt△ABC中,AB=10,sinA=0.6,把Rt△ABC绕着直线AC旋转一周,求所得圆锥的侧面展开图的弧长、圆心角、面积.