题目内容
 如图,在⊙O中,AB,CD是直径.
如图,在⊙O中,AB,CD是直径.(1)AD与BC平行吗?说说你的理由;
(2)四边形ADBC矩形吗?为什么?
考点:圆周角定理,矩形的判定
专题:
分析:(1)根据圆周角定理得到∠DAB=∠BCD,加上∠DAO=∠ODA,则∠ADO=∠BCD,于是根据平行线的判定方法得到AD∥BC;
(2)利用对角线互相平分且相等的四边形是矩形进行判断.
(2)利用对角线互相平分且相等的四边形是矩形进行判断.
解答:解:(1)AD与BC平行.理由如下:
∵AB,CD是直径,
∴∠DAB=∠BCD,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠ADO=∠BCD,
∴AD∥BC;
(2)∵AB,CD是直径,
∴OD=OA=OC=OB,
∴四边形ACBD为矩形.
∵AB,CD是直径,
∴∠DAB=∠BCD,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠ADO=∠BCD,
∴AD∥BC;
(2)∵AB,CD是直径,
∴OD=OA=OC=OB,
∴四边形ACBD为矩形.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
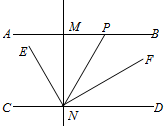 如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究
如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究 如图,AE平分∠BAC,FD⊥BC.求证:∠EFD=
如图,AE平分∠BAC,FD⊥BC.求证:∠EFD= 如图,一艘货轮以36km的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续向北航行40min后到达C点,发现灯塔B在塔北偏东75°方向,求此时货轮与灯塔B的距离(结果精确到0.01海里).
如图,一艘货轮以36km的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续向北航行40min后到达C点,发现灯塔B在塔北偏东75°方向,求此时货轮与灯塔B的距离(结果精确到0.01海里).