题目内容
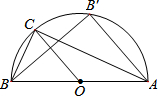 如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c>
如图,△ABC内接于⊙O,∠ACB=90°,BC=a,AB=c(c>| 2 |
考点:垂径定理,勾股定理,三角形中位线定理
专题:计算题
分析:根据圆周角定理,由∠ACB=90°得到AB为⊙O的直径,再利用圆对称的性质点B′在⊙O上,且OC⊥BB′,根据垂径定理得
=
,于是利用圆周角定理得到∠BAC=∠CBB′,则可判断Rt△ABC∽△BCD,利用相似比可表示出CD=
,所以OD=OC-CD=
-
=
,然后证明OD为△ABB′的中位线,利用三角形中位线性质计算AB′.
 |
| BC |
 |
| B′C |
| a2 |
| c |
| c |
| 2 |
| a2 |
| c |
| c2-2a2 |
| 2c |
解答: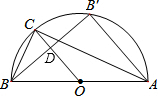 解:∵△ABC内接于⊙O,∠ACB=90°,
解:∵△ABC内接于⊙O,∠ACB=90°,
∴AB为⊙O的直径,
∵B关于OC的对称点为B′,
∴点B′在⊙O上,OC⊥BB′,
∴
=
,
∴∠BAC=∠CBB′,
∴Rt△ABC∽△BCD,
∴
=
,即
=
,
∴CD=
,
∴OD=OC-CD=
-
=
,
∵AB为直径,
∴∠AB′B=90°,
∴OD∥AB′,
而OA=OB,
∴OD为△ABB′的中位线,
∴AB′=2OD=
.
故答案为
.
 解:∵△ABC内接于⊙O,∠ACB=90°,
解:∵△ABC内接于⊙O,∠ACB=90°,∴AB为⊙O的直径,
∵B关于OC的对称点为B′,
∴点B′在⊙O上,OC⊥BB′,
∴
 |
| BC |
 |
| B′C |
∴∠BAC=∠CBB′,
∴Rt△ABC∽△BCD,
∴
| BC |
| CD |
| AB |
| BC |
| a |
| CD |
| c |
| a |
∴CD=
| a2 |
| c |
∴OD=OC-CD=
| c |
| 2 |
| a2 |
| c |
| c2-2a2 |
| 2c |
∵AB为直径,
∴∠AB′B=90°,
∴OD∥AB′,
而OA=OB,
∴OD为△ABB′的中位线,
∴AB′=2OD=
| c2-2a2 |
| c |
故答案为
| c2-2a2 |
| c |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了相似三角形的判定与性质、圆周角定理和三角形中位线性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AD,BF分别是△ABC的高与角平分线,BF,AD交于E,∠1=∠2,求证:AB⊥AC.
如图,AD,BF分别是△ABC的高与角平分线,BF,AD交于E,∠1=∠2,求证:AB⊥AC.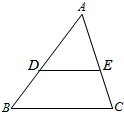 (1)如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,
(1)如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,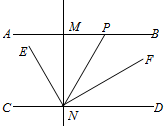 如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究
如图,直线AB∥CD,MN⊥AB于M交CD于M交CD于N,P为射线MF上一动点,连接NP,NE平分∠CNP,NF⊥NE,当点P运动时,请你探究
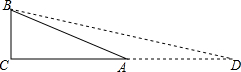 小明是一个非常喜欢动脑筋肯钻研的同学,学习了特殊角的三角函数值后,他进行了如下探究:根据tan30°=
小明是一个非常喜欢动脑筋肯钻研的同学,学习了特殊角的三角函数值后,他进行了如下探究:根据tan30°=