题目内容
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
(1)当点E为AB的中点时,如图1,求证:EC=ED;
(2)当点E不是AB的中点时,如图2,过点E作EF∥BC,求证:△AEF是等边三角形;
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.

(1)当点E为AB的中点时,如图1,求证:EC=ED;
(2)当点E不是AB的中点时,如图2,过点E作EF∥BC,求证:△AEF是等边三角形;
(3)在第(2)小题的条件下,EC与ED还相等吗,请说明理由.

考点:等边三角形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)根据等边三角形三线合一的性质可得∠ECB=30°,∠ABC=60°,根据AE=EB=BD,可得∠ECB=
∠ACB=30°,∠EDB=∠DEB=
∠ACB=30°,根据等角对等边即可证得结论;
(2)根据平行线的性质证得∠AEF=∠ABC=60°,∠AFE=∠C=60°,即可证得结论;
(3)先求得BE=FC,然后证得△DBE≌△EFC即可;
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据平行线的性质证得∠AEF=∠ABC=60°,∠AFE=∠C=60°,即可证得结论;
(3)先求得BE=FC,然后证得△DBE≌△EFC即可;
解答: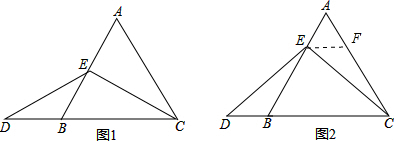 证明:(1)如图1,在等边△ABC中,AB=BC=AC,
证明:(1)如图1,在等边△ABC中,AB=BC=AC,
∴∠ABC=∠ACB=∠A=60°,
∵AE=EB=BD,
∴∠ECB=
∠ACB=30°,∠EDB=∠DEB=
∠ACB=30°,
∴∠EDB=∠ECB,
∴EC=ED;
(2)如图2,∵EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠C=60°,
∴△AEF为等边三角形;
(3)EC=ED;
理由:∵∠AEF=∠ABC=60°,
∴∠EFC=∠DBE=120°,
∵AB=AC,AE=AF,
∴AB-AE=AC-AF,即BE=FC,
在△DBE和△EFC中,
,
∴△DBE≌△EFC(SAS),
∴ED=EC.
 证明:(1)如图1,在等边△ABC中,AB=BC=AC,
证明:(1)如图1,在等边△ABC中,AB=BC=AC,∴∠ABC=∠ACB=∠A=60°,
∵AE=EB=BD,
∴∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDB=∠ECB,
∴EC=ED;
(2)如图2,∵EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠C=60°,
∴△AEF为等边三角形;
(3)EC=ED;
理由:∵∠AEF=∠ABC=60°,
∴∠EFC=∠DBE=120°,
∵AB=AC,AE=AF,
∴AB-AE=AC-AF,即BE=FC,
在△DBE和△EFC中,
|
∴△DBE≌△EFC(SAS),
∴ED=EC.
点评:本题考查了等边三角形的判定和性质性质,平行线的性质,三角形全等的判定和性质,熟练掌握性质和定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
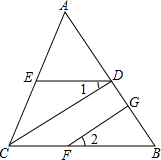 如图,已知DE∥BC,FG⊥AB,垂足为G,∠1=∠2.
如图,已知DE∥BC,FG⊥AB,垂足为G,∠1=∠2.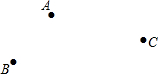 作图题(要求:尺规作图,不写作法,保留作图痕迹)如图,平面上有三个村庄A、B、C,现计划打一水井P,使水井P到三个村庄的距离相等.
作图题(要求:尺规作图,不写作法,保留作图痕迹)如图,平面上有三个村庄A、B、C,现计划打一水井P,使水井P到三个村庄的距离相等.