题目内容
2.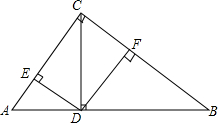 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于E,DF⊥BC于F.若AC=3,AB=5,求DE:DF的值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于E,DF⊥BC于F.若AC=3,AB=5,求DE:DF的值.
分析 根据已知条件得到△ACD∽△BCD,然后由相似三角形的性质:相似三角形对应边的高等于相似比即可得到结论.
解答 解:∵∠ACB=90°,CD⊥AB于点D,
∴∠ACB=∠ADC=∠BDC=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△BCD,
∵DE⊥AC于E,DF⊥BC于F,
∴$\frac{DE}{DF}=\frac{AC}{BC}$=$\frac{3}{4}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.如果下列各组数是三角形的三边长,那么不能组成直角三角形的一组为( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 12,15,25 | D. | 0.7,2.4,2.5 |
13. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
12.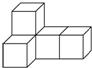 如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
 如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )
如图是由五个大小相同的正方体搭成的几何体,则关于它从三个方向看所得到的形状图,下列说法正确的是( )| A. | 从正面看所得到的形状图的面积最小 | |
| B. | 从左面看所得到的形状图的面积最小 | |
| C. | 从上面看所得到的形状图的面积最小 | |
| D. | 从三个方向看所得到的形状图的面积一样大 |
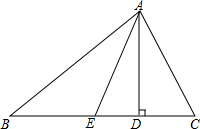 如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论:
如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论: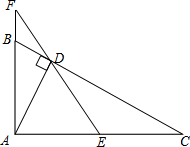 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证: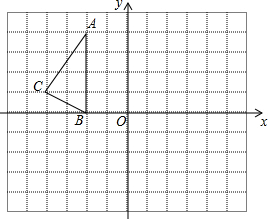 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题: