题目内容
17.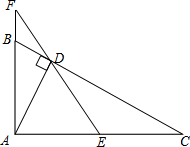 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:(1)△DFB∽△AFD;
(2)AB:AC=DF:AF.
分析 (1)由已知条件得到∠BAC=∠ADB=90°,根据余角的性质得到∠BAD=∠C,由直角三角形的性质和对顶角相等得到∠BAD=∠BDF,即可得到结论;
(2)根据已知条件推出△ABD∽△CAD;于是得到$\frac{AB}{AC}$=$\frac{BD}{AD}$,由于△DFB∽△AFD;于是得到$\frac{BD}{AD}=\frac{DF}{AF}$,等量代换即可得到结论.
解答 解:(1)∵∠BAC=90°,AD⊥BC于D,
∴∠BAC=∠ADB=90°,
∴∠BAD+∠ABD=∠ABD+∠C=90°,
∴∠BAD=∠C,
∵E是AC的中点,
∴DE=CE,
∴∠C=∠EDC,
∵∠EDC=∠BDF,
∴∠BAD=∠BDF,
∵∠F=∠F,
∴△DFB∽△AFD;
(2)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠BAD+∠DAC=90°,∠DAC+∠ACD=90°,
∴∠BAD=∠ACD,
∵∠ADB=∠ADC,
∴△ABD∽△CAD;
∴$\frac{AB}{AC}$=$\frac{BD}{AD}$,
∵△DFB∽△AFD;
∴$\frac{BD}{AD}=\frac{DF}{AF}$,
∴AB:AC=DF:AF.
点评 此题考查了相似三角形的判定与性质以及直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
7. 如图,在△ABC中,AB=AC,AD=AE,则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,AD=AE,则图中全等三角形的对数是( )
 如图,在△ABC中,AB=AC,AD=AE,则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,AD=AE,则图中全等三角形的对数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
 如图,已知在△ABC中,两条内角平分线BD、CE相交于点O,若∠BOC=110°,则∠A=40度.
如图,已知在△ABC中,两条内角平分线BD、CE相交于点O,若∠BOC=110°,则∠A=40度.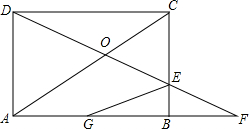 如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).
如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).
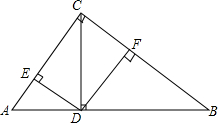 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于E,DF⊥BC于F.若AC=3,AB=5,求DE:DF的值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥AC于E,DF⊥BC于F.若AC=3,AB=5,求DE:DF的值.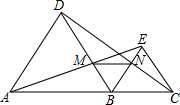 如图,A、B、C三点在同一直线上,△ABD和△BCE都是等边三角形,
如图,A、B、C三点在同一直线上,△ABD和△BCE都是等边三角形,