题目内容
2.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a-b+c=0,我们称这个方程为“阿凡达”方程.已知ax2+bx+c=0是阿凡达方程,且有两个相等的实数根,则下列正确的是( )| A. | a=b | B. | a=c | C. | a=2b=c | D. | b=c |
分析 因为方程有两个相等的实数根,所以根的判别式△=b2-4ac=0,又a-b+c=0,即b=a+c,代入b2-4ac=0得(a+c)2-4ac=0,化简即可得到a与c的关系.
解答 解:∵一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,
∴△=b2-4ac=0,
又∵a-b+c=0,
∴b=a+c,
代入b2-4ac=0得(a+c)2-4ac=0,
化简得(a-c)2=0,
所以a=c.
故选B.
点评 此题主要考查了一元二次方程根的情况与判别式△的关系,关键是熟练掌握:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
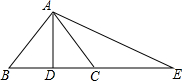 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.