题目内容
17．计算下列各式的值：（1）（$\sqrt{3}$+$\sqrt{2}$）-$\sqrt{2}$
（2）（-3）2-|-$\frac{1}{2}$|+$\frac{1}{2}$-$\sqrt{9}$
（3）x2-121=0；
（4）（x-5）3+8=0．
分析 （1）原式去括号合并即可得到结果；
（2）原式第一项利用乘方的意义化简，第二项利用绝对值的代数意义化简，最后一项利用算术平方根定义计算即可得到结果；
（3）方程变形后，利用平方根定义开方即可求出解；
（4）方程变形后，利用立方根定义开立方即可求出解．
解答 解：（1）原式=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{2}$=$\sqrt{3}$；
（2）原式=9-$\frac{1}{2}$+$\frac{1}{2}$-3=6；
（3）方程变形得：x2=121，
开方得：x=±11；
（4）方程变形得：（x-5）3=-8，
开立方得：x-5=-2，
解得：x=3．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
优加精卷系列答案
相关题目
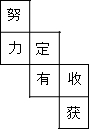水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“定”在正方体的前面，那么这个正方体的后面是（ ）
如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，在中间长为（a+b）的正方形空地上将修建一座雕像，规划部门计划将阴影部分进行绿化，则绿化的面积是多少平方米？并求出当a=5，b=3时的绿化面积．
12．下列算式：
（1）$\sqrt{2}+\sqrt{5}=\sqrt{7}$
（2）$5\sqrt{x}-2\sqrt{x}=3\sqrt{x}$
（3）$\frac{{\sqrt{8}+\sqrt{50}}}{2}=\sqrt{4}+\sqrt{25}=7$
（4）$3\sqrt{3a}+\sqrt{27a}=6\sqrt{3a}$
其中正确的是（ ）
（1）$\sqrt{2}+\sqrt{5}=\sqrt{7}$
（2）$5\sqrt{x}-2\sqrt{x}=3\sqrt{x}$
（3）$\frac{{\sqrt{8}+\sqrt{50}}}{2}=\sqrt{4}+\sqrt{25}=7$
（4）$3\sqrt{3a}+\sqrt{27a}=6\sqrt{3a}$
其中正确的是（ ）
| A． | （1）和（3） | B． | （2）和（4） | C． | （3）和（4） | D． | 1）和（4） |
