题目内容
16.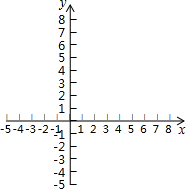 小东根据学习一次函数的经验,对函数y=|2x-1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
小东根据学习一次函数的经验,对函数y=|2x-1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:(1)函数y=|2x-1|的自变量x的取值范围是全体实数;
(2)已知:
①当x=$\frac{1}{2}$时,y=|2x-1|=0;
②当x>$\frac{1}{2}$时,y=|2x-1|=2x-1
③当x<$\frac{1}{2}$时,y=|2x-1|=1-2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m=3;n=5;:
| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
(5)根据函数的图象,写出函数y=|2x-1|的一条性质.
分析 (1)函数y=|2x-1|的自变量x的取值范围是全体实数;
(3)取m=3,把x=3代入y=|2x-1|计算即可;
(4)根据(3)中的表格描点连线即可;
(5)根据函数的图象,即可求解.
解答 解:(1)函数y=|2x-1|的自变量x的取值范围是全体实数;
故答案为全体实数; (3)m、n的取值不唯一,取m=3,
(3)m、n的取值不唯一,取m=3,
把x=3代入y=|2x-1|,得y=|2×3-1|=5,
即m=3,n=5.
故答案为3,5;
(4)图象如右:
(5)当x=$\frac{1}{2}$时,函数y=|2x-1|有最小值0.
点评 本题考查了一次函数的图象与性质,掌握一次函数的性质是解题的关键.

练习册系列答案
相关题目
17.已知直线y=mx+n(m,n为常数)经过点(0,-2)和(3,0),则关于x的方程mx+n=0的解为( )
| A. | x=3 | B. | x=-2 | C. | x=2 | D. | x=0 |
18.为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
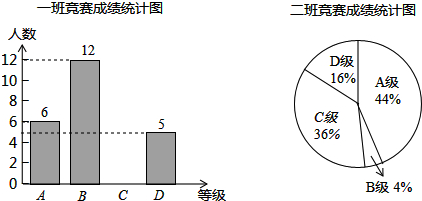
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.

(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
| 平均数(分) | 中位数(分) | 众数(分) | 方差 | |
| 一班 | a | b | 90 | 106.24 |
| 二班 | 87.6 | 80 | c | 138.24 |
6.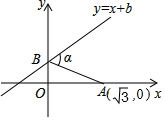 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )| A. | 3$\sqrt{3}$-3 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+3 | D. | 2$\sqrt{3}$-3 |
 如图所示,已知∠1+∠2=180°,∠B=∠D,AD平分∠EAC,那么CB平分∠ACF吗?为什么?
如图所示,已知∠1+∠2=180°,∠B=∠D,AD平分∠EAC,那么CB平分∠ACF吗?为什么?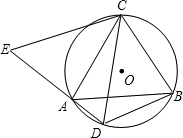 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中$\widehat{AB}$上一点,延长DA至点E,使CE=CD.