题目内容
4．已知函数y=$\left\{\begin{array}{l}{-（x-1）^{2}+1（x≤3）}\\{-（x-5）^{2}+1（x＞3）}\end{array}\right.$，若使y=k成立的x值恰好有两个，则k的取值范围为k=1或k＜-3．分析 首先在平面直角坐标系内作出函数y=$\left\{\begin{array}{l}{-（x-1）^{2}+1（x≤3）}\\{-（x-5）^{2}+1（x＞3）}\end{array}\right.$的图象，然后利用数形结合的方法即可找到使y=k成立的x值恰好有2个的k值．
解答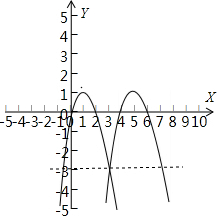 
解：画函数y=$\left\{\begin{array}{l}{-（x-1）^{2}+1（x≤3）}\\{-（x-5）^{2}+1（x＞3）}\end{array}\right.$的图象：
根据图象知道当y=1或y＜-3时，对应成立的x有恰好有2个，
所以k=1或k＜-3．
故答案为：k=1或k＜-3．
点评 此题主要考查了利用二次函数的图象解决交点问题，解题的关键是把解方程的问题转换为根据函数图象找交点的问题．
练习册系列答案
相关题目
5．在同一平面内已知∠AOB=80°，∠BOC=20°，OM、ON分别是∠AOB和∠BOC的平分线，则∠MON的度数为（ ）
| A． | 30° | B． | 40° | C． | 50° | D． | 30°或50° |
6．
如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（ ）
如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（ ）| A． | 2cm2 | B． | 1cm2 | C． | $\frac{1}{4}$cm2 | D． | $\frac{1}{2}$cm2 |
3．一个盒子装有除颇色外其它均相同的2个红球和3个白球，现从中任取2个球．则取到的是一个红球、一个白球的概率为（ ）
| A． | 0.2 | B． | 0.3 | C． | 0.4 | D． | 0.6 |
10．下列计算，正确的是（ ）
| A． | （-2）-2=4 | B． | 20×2-3=-$\frac{1}{8}$ | C． | 46÷（-2）6=64 | D． | $\sqrt{6}$-$\sqrt{2}$=2 |
16．
小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：
（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
（4）在平面直角坐标系xOy中，作出函数y=|2x-1|的图象；
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
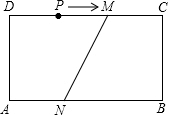如图，矩形ABCD中，AB=12cm，BC=4cm，DM=8cm，AN=5cm．点P在CD边上．