题目内容
5．有些大数值问题可以通过“用字母代替数”转为成整式问题来解决，请先阅读下面的解题过程，再解答后面的问题．例：若x=123456789×123456786，y=123456788×123456787，试求x-y的值．
解：设123456788=a，
则x=a（a-3）=a2-3a，y=（a-1）（a-2）=a2-3a+2，
∴x-y=（a2-3a）-（a2-3a+2）=a2-3a-a2+3a-2=-2
你能用这种方法解答后面的问题吗？
计算：0.135×2.1352-0.1353-0.272．
分析 根据题目中的例题，不拿发现所求式子中，可以设0.135=a，然后根据完全平方公式、单项式乘多项式、合并同类项可以对题目中的式子化简，然后将a=0.135代入即可求得所求式子的值，本题得以解决．
解答 解：设0.135=a，
则0.135×2.1352-0.1353-0.272
=a×（2+a）2-a3-（2a）2
=a（4+4a+a2）-a3-4a2
=4a+4a2+a3-a3-4a2
=4a，
将a=0.135代入，原式=4×0.135=0.54．
点评 本题考查整式的混合运算、换元法，解题的关键是明确题目中的例子的计算方法和整式的混合运算的计算方法．
练习册系列答案
相关题目
6．
如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（ ）
如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（ ）| A． | 2cm2 | B． | 1cm2 | C． | $\frac{1}{4}$cm2 | D． | $\frac{1}{2}$cm2 |
16．
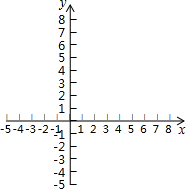小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：
（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
（4）在平面直角坐标系xOy中，作出函数y=|2x-1|的图象；
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
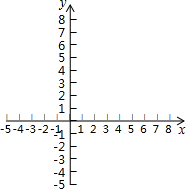小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
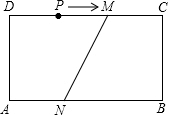如图，矩形ABCD中，AB=12cm，BC=4cm，DM=8cm，AN=5cm．点P在CD边上．
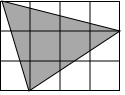如图由12个相同小正方形组成一个长方形．
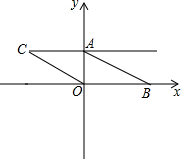如图．已知在平面直角坐标系中．点A（0，m），点B（n，0），D（2m，n），且m、n满足（m-2）2+$\sqrt{n-4}$=0，将线段AB向左平移，使点B与点O重合，点C与点A对应．