题目内容
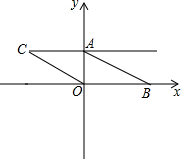
6．
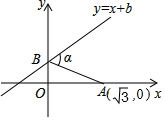如图，已知A点坐标为（$\sqrt{3}$，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=60°，则b的值为（ ）| A． | 3$\sqrt{3}$-3 | B． | $\sqrt{3}$+3 | C． | 2$\sqrt{3}$+3 | D． | 2$\sqrt{3}$-3 |
分析 令直线y=x+b与x轴交于点C，根据直线的解析式可求出点B、C的坐标，进而得出∠BCO=45°，再通过角的计算得出∠BAO=15°，以BA为边在∠ABO内部作∠ABD=∠BAO=15°，可设AD=BD=x，得OD=OA-AD=$\sqrt{3}$-x，在Rt△BOD中根据cos∠BDO=$\frac{OD}{BD}$求得x，即可得BD的长，再根据BO=BDsin∠BDO可得答案．
解答 解：令直线y=x+b与x轴交于点C，
令y=x+b中x=0，则y=b，
∴B（0，b）；
令y=x+b中y=0，则x=-b，
∴C（-b，0）．
∴∠BCO=45°．
∵α=∠BCO+∠BAO=60°，
∴∠BAO=15°，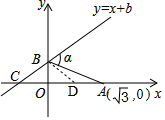
如图，以BA为边在∠ABO内部作∠ABD=∠BAO=15°，
设AD=BD=x，
∴OD=OA-AD=$\sqrt{3}$-x，
在Rt△BOD中，∵∠BDO=∠ABD+∠BAO=30°，
∴cos∠BDO=$\frac{OD}{BD}$，即$\frac{\sqrt{3}-x}{x}$=$\frac{\sqrt{3}}{2}$，
解得：x=4$\sqrt{3}$-6，即BD=4$\sqrt{3}$-6，
∴BO=BDsin∠BDO=（4$\sqrt{3}$-6）×$\frac{1}{2}$=2$\sqrt{3}$-3，
故选：D．
点评 本题主要考查三角形的外角性质、特殊角的三角函数值以及一次函数的斜率的几何意义．解题时，注意挖掘隐含在题干中的已知条件∠BCA=45°及在直角三角形中构造30°的内角是解题的关键．
练习册系列答案
相关题目
16．
小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：
（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
（4）在平面直角坐标系xOy中，作出函数y=|2x-1|的图象；
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
小东根据学习一次函数的经验，对函数y=|2x-1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：（1）函数y=|2x-1|的自变量x的取值范围是全体实数；
（2）已知：
①当x=$\frac{1}{2}$时，y=|2x-1|=0；
②当x＞$\frac{1}{2}$时，y=|2x-1|=2x-1
③当x＜$\frac{1}{2}$时，y=|2x-1|=1-2x；
显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m=3；n=5；：
| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
（5）根据函数的图象，写出函数y=|2x-1|的一条性质．
如图．已知在平面直角坐标系中．点A（0，m），点B（n，0），D（2m，n），且m、n满足（m-2）2+$\sqrt{n-4}$=0，将线段AB向左平移，使点B与点O重合，点C与点A对应．
RT△ABC中，∠ABC=30°，CD⊥AB，将△ACD绕A旋转至△AC′D′，连接D′C，M、N分别是BC′和D′C的中点，连接MN，探索D′C和MN的数量及位置关系．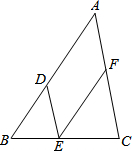
请在下列括号里填上合适的理由：