题目内容
18.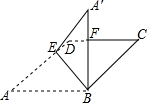 如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)
如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)
分析 先根据Rt△BCF中,sin∠C=$\frac{BF}{BC}$,求得BF≈2.6,再根据A'B=4,即可得到线段A′F的长.
解答 解:∵A′B⊥CD,BC=4,
∴Rt△BCF中,sin∠C=$\frac{BF}{BC}$,
∴sin40°=$\frac{BF}{4}$,
即0.643≈$\frac{BF}{4}$,
∴BF≈2.6,
又∵A'B=AB=BC=4,
∴A'F=A'B-BF=4-2.6=1.4,
∴线段A′F的长约为1.4cm.
点评 本题主要考查了折叠问题,以及菱形的性质,解直角三角形的综合应用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.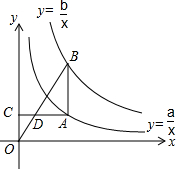 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
7.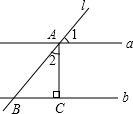 如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
 如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )
如图,直线a∥b,直线l与a,b分别交于点A,B,过点A作AC⊥b于点C,若∠1=50°,则∠2的度数为( )| A. | 130° | B. | 50° | C. | 40° | D. | 25° |
 甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.
甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.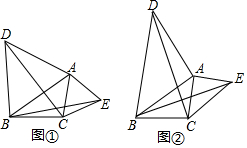
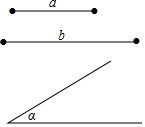 已知:线段a、b、∠α(如图),用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a、b,且两条对角线所成的一个角等于∠α.
已知:线段a、b、∠α(如图),用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a、b,且两条对角线所成的一个角等于∠α.
 如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.
如图,?ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF=AD.