题目内容
3.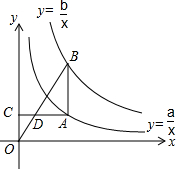 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
分析 过点B作BE⊥y轴于E,延长线段BA,交x轴于F,得出四边形AFOC是矩形,四边形OEBF是矩形,得出S矩形AFOC=a,S矩形OEBF=b,根据平行线分线段成比例定理证得AB=2OC,即OE=3OC,即可求得b=3a,从而求得3a-b=0.
解答  解:过点B作BE⊥y轴于E,延长线段BA,交x轴于F,
解:过点B作BE⊥y轴于E,延长线段BA,交x轴于F,
∵AB∥y轴,
∴BF⊥x轴,
∴四边形BFOE是矩形,四边形OFAC是矩形,
∴AF=OC,BF=OE,
∴AB=CE,
∵点A在双曲线y=$\frac{a}{x}$(x>0)上,
∴S矩形AFOC=a,
同理S矩形OFBE=b,
∵AB∥OE,AD=2DC,
∴$\frac{OC}{AB}$=$\frac{CD}{AD}$=$\frac{1}{2}$,
∴AB=2OC,
∴CE=2OD,
∴S矩形OEBF=3S矩形AFOC,
∴b=3a,
∴3a-b=0,
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,矩形的判定和性质,平行线分线段成比例定理,作出辅助线,构建矩形是解题的关键.

练习册系列答案
相关题目
8.2016年是雾霾肆虐的一年,河南更是雾霾重灾区,为减少雾霾对人体的伤害,某企业计划购进一批防霾口罩免费发放给学生使用,现甲、乙两个口罩厂有相同的防霾口罩可供选择,其具体销售方案如下:
设购买防霾口罩x个,到两家口罩厂购买所需费用分别为y甲(元),y乙(元).
(1)该企业发现若从两厂分别购买防霾口罩各2500个共花费9750元,若从两厂分别购买防霾口罩各3000个共花费11600元,请求出m,n的值;
(2)分别求出y甲,y乙与x之间的函数关系式;
(3)如果你是该企业的负责人,你认为到哪家口罩厂购买防霾口罩才合算,为什么?
| 甲口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过1000个时 | 2元/个 |
| 超过1000个的部分 | m元/个 |
| 乙口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过2000个时 | 2元/个 |
| 超过2000个的部分 | n元/个 |
(1)该企业发现若从两厂分别购买防霾口罩各2500个共花费9750元,若从两厂分别购买防霾口罩各3000个共花费11600元,请求出m,n的值;
(2)分别求出y甲,y乙与x之间的函数关系式;
(3)如果你是该企业的负责人,你认为到哪家口罩厂购买防霾口罩才合算,为什么?
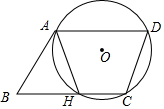 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.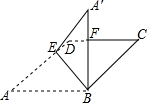 如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)
如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm) 如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )
如图,矩形ABCD的顶点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,顶点B、C在x轴上,对角线DB的延长线交y轴于点E,连接CE,若△BCE的面积是6,则k的值为( )