题目内容
11. 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
分析 如图,OA=80cm,OB=60cm,AB为太阳光线,利用勾股定理可计算出AB=100,利用平行投影,当OA旋转到与太阳光线垂直时,此时木棒的影子最长,接着证明△AOB∽△OA′B′,然后利用相似比求出OB′即可.
解答 解:如图,OA=80cm,OB=60cm,AB为太阳光线,则AB=$\sqrt{6{0}^{2}+8{0}^{2}}$=100,
当OA旋转到与太阳光线垂直时,此时木棒的影子最长,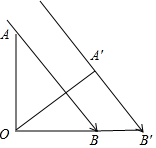
即OA′⊥A′B′(A′B′为太阳光线),
∵AB∥A′B′,
∴∠ABO=∠A′B′O,
∴△AOB∽△OA′B′,
∴OA:OA′=AB:OB′,
∴OB′=AB=100(cm),
答:该木棒转到与太阳光线垂直位置时影子最长,此时影子的长度为100cm.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
1.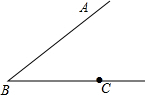 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点
(1)按下列要求进行尺规作图:
①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点(1)按下列要求进行尺规作图:
①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
19.在平行四边形、菱形、矩形、正方形中,能使一个点到各顶点距离相等的图形是( )
| A. | 菱形和矩形 | B. | 菱形和正方形 | ||
| C. | 矩形和正方形 | D. | 平行四边形和菱形 |
20.若(x+m)与(x+$\frac{1}{3}$)的积不含x项,则m的值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
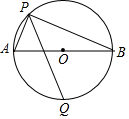 如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$.
如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$.