��Ŀ����
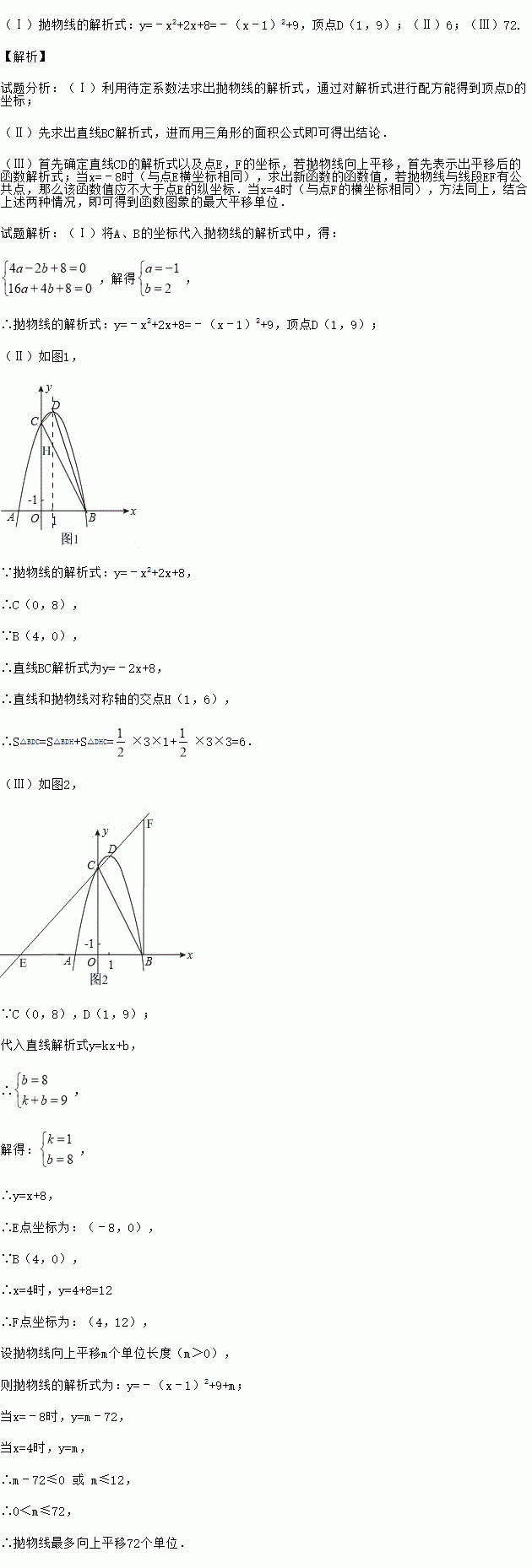
��ͼ����֪���κ���y=ax2+bx+8��a��0����ͼ����x�ύ�ڵ�A����2��0����
B��4��0����y�ύ�ڵ�C��
�����������ߵĽ���ʽ���䶥��D�����ꣻ
�������BCD�������
������ֱ��CD��x�����E������B��x��Ĵ��ߣ���ֱ��CD���F��������������Գ�������ƽ�ƣ�ʹ���������߶�EF���й����㣮��̽������������������ƽ�ƶ��ٸ���λ���ȣ�ֱ��д���������д�����̣���
 ���������ߵĽ���ʽ��y=��x2+2x+8=����x��1��2+9������D��1��9��������6������72.
��������
����������������ô���ϵ������������ߵĽ���ʽ��ͨ���Խ���ʽ�����䷽�ܵõ�����D�����ꣻ
���������ֱ��BC����ʽ�������������ε������ʽ���ɵó����ۣ�
��������ȷ��ֱ��CD�Ľ���ʽ�Լ���E��F�����꣬������������ƽ�ƣ����ȱ�ʾ��ƽ�ƺ�ĺ�������ʽ����x...
���������ߵĽ���ʽ��y=��x2+2x+8=����x��1��2+9������D��1��9��������6������72.
��������
����������������ô���ϵ������������ߵĽ���ʽ��ͨ���Խ���ʽ�����䷽�ܵõ�����D�����ꣻ
���������ֱ��BC����ʽ�������������ε������ʽ���ɵó����ۣ�
��������ȷ��ֱ��CD�Ľ���ʽ�Լ���E��F�����꣬������������ƽ�ƣ����ȱ�ʾ��ƽ�ƺ�ĺ�������ʽ����x...
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д���ͼ��������С����Ǧ���¼����м�������������Ǧ���н��߶�y(m)��ˮƽ����x(m)֮��Ĺ�ϵΪy���� (x��4)2��3���ɴ˿�֪Ǧ���Ƴ��ľ�����___________.
(x��4)2��3���ɴ˿�֪Ǧ���Ƴ��ľ�����___________.

 10
����������������
���У���y=0���ã���ã�x1=10��x2=��2����ȥ������Ǧ���Ƴ��ľ�����10m���ʴ�Ϊ��10��
10
����������������
���У���y=0���ã���ã�x1=10��x2=��2����ȥ������Ǧ���Ƴ��ľ�����10m���ʴ�Ϊ��10�� ijһ�ͺŷɻ���½���еľ���y(��λ��m)�뻬��ʱ��x(��λ��s)֮��ĺ�����ϵʽ��y��60x��1.5x2�����ͺŷɻ���½���軬��________m����ͣ������
 600
�������������������y=60x��1.5x2=��1.5��x��20��2+600��
��x=20ʱ��yȡ�����ֵ����ʱy=600
600
�������������������y=60x��1.5x2=��1.5��x��20��2+600��
��x=20ʱ��yȡ�����ֵ����ʱy=600 ��ͼ��O�DZ߳�Ϊa��������ABCD�����ģ���һ��뾶�㹻����Բ��Ϊֱ�ǵ�����ֽ���Բ�ķ���O�㴦������ֽ���Բ����O��ת����������ABCD��ֽ�帲�Dz��ֵ����Ϊ��������
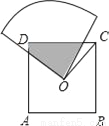
A.  a2 B.
a2 B.  a2 C.
a2 C.  a2 D.
a2 D. 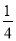 a
a
 B
����������������
���εİ뾶��AD��E����CD��F������OD����ͼ��
���ı���ABCDΪ�����Σ���OD=OC����COD=90�㣬��ODA=��OCD=45�㣮
�ߡ�EOF=90�㣬����EOD+��DOF=90�㣬��DOF+��COF=90�㣬���EOD=��FOC��
�ڡ�ODE�͡�OCF�У��ߡ�ODE=��OCF��OD=OC����EOD=��COF�����ODE�ա�OCF����S��OD...
B
����������������
���εİ뾶��AD��E����CD��F������OD����ͼ��
���ı���ABCDΪ�����Σ���OD=OC����COD=90�㣬��ODA=��OCD=45�㣮
�ߡ�EOF=90�㣬����EOD+��DOF=90�㣬��DOF+��COF=90�㣬���EOD=��FOC��
�ڡ�ODE�͡�OCF�У��ߡ�ODE=��OCF��OD=OC����EOD=��COF�����ODE�ա�OCF����S��OD... һ��ͼ�����۾���ƽ�Ʊ任�����Ǿ�����ת�任������˵����ȷ���ǣ�������
�ٶ�Ӧ�߶�ƽ��
�ڶ�Ӧ�߶����
��ͼ�ε���״�ʹ�С��û�з����仯
�ܶ�Ӧ����ȣ�
A. �٢ڢ� B. �ڢۢ� C. �٢ڢ� D. �٢ۢ�
 B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
��ѡB��
B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
��ѡB�� ��ͼ�����κ���y=ax2��4x+c��ͼ������ԭ�㣬��x�ύ�ڵ�A����4��0����

��1������κ����Ľ���ʽ��
��2�����������ϴ��ڵ�P������S��AOP=8����ֱ��д����P�����꣮
 ��1��y������4x P1����2�� 4����P2����2��2����4����P3����2��2����4��
�������������������1���ѵ�Aԭ���������뺯������ʽ�����ô���ϵ��������κ�������ʽ���
��2�����������ε������ʽ�����P��AO�ľ��룬Ȼ��ֵ�P��x����Ϸ����·����������ɣ�
�����������1������֪�����ã�
��ã�
���ԣ��˶��κ����Ľ���ʽΪy=��x2��4x��
...
��1��y������4x P1����2�� 4����P2����2��2����4����P3����2��2����4��
�������������������1���ѵ�Aԭ���������뺯������ʽ�����ô���ϵ��������κ�������ʽ���
��2�����������ε������ʽ�����P��AO�ľ��룬Ȼ��ֵ�P��x����Ϸ����·����������ɣ�
�����������1������֪�����ã�
��ã�
���ԣ��˶��κ����Ľ���ʽΪy=��x2��4x��
... ��ͼ�Ƕ��κ���y=ax2+bx+c�IJ���ͼ����ͼ���֪����ʽax2+bx+c��0�Ľ⼯�ǣ�������
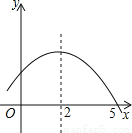
A. -1��x��5 B. x��5 C. x��-1��x��5 D. x��-1��x��5
 D
����������ͼ��֪�������ߵĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��5��0����
�ຯ��ͼ����x�����һ��������Ϊ��-1��0����
��ax2+bx+c��0�Ľ⼯��x��-1��x��5��
��ѡC.
D
����������ͼ��֪�������ߵĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��5��0����
�ຯ��ͼ����x�����һ��������Ϊ��-1��0����
��ax2+bx+c��0�Ľ⼯��x��-1��x��5��
��ѡC. ����������˵������������������κ������ǵĺʹ���90�㣻�ڵ���������һ������������Σ��۵�����������һ����ǵ���120�㣬���������һ���ǵȱ������Σ��ܵ�������������һ����40�㣬��ô���ĵ���70�㣻��һ����������������һ���Dz�С��60�ȣ�������ȷ���У�������
A. 2�� B. 3�� C. 4�� D. 5��
 B
�����������У��ض���ȷ����������ǵĺͲ�����90�㣬��������ڽǽ����ڻ����90�㣬�������ν�������������Σ����У�����������ܻ����������������εĶ����Ƕ۽�ʱ�����������Ƕ۽������Σ��ʴ����У���������������һ����ǵ���120�㣬�������������һ���ڽǵ���60�㣬�����������һ���ǵȱ������Σ�����ȷ�����У�����Ӧ��Ϊ����������ǿ�����40���70�㣬�ʴ����У���Ȼ��ȷ�������...
B
�����������У��ض���ȷ����������ǵĺͲ�����90�㣬��������ڽǽ����ڻ����90�㣬�������ν�������������Σ����У�����������ܻ����������������εĶ����Ƕ۽�ʱ�����������Ƕ۽������Σ��ʴ����У���������������һ����ǵ���120�㣬�������������һ���ڽǵ���60�㣬�����������һ���ǵȱ������Σ�����ȷ�����У�����Ӧ��Ϊ����������ǿ�����40���70�㣬�ʴ����У���Ȼ��ȷ�������... ���и�ʽ�У�����ƽ���ʽ��ʽ�ֽ���ǣ��� ����
A. x2+x B. x2+8x+16 C. x2+4 D. x2��1
 D
��������A. x²+x=x(x+1)������ȡ����ʽ���ֽ���ʽ���ʴ�ѡ�����
B. x²+8x+16=(x+4)²���ǹ�ʽ���ֽ���ʽ���ʴ�ѡ�����
C. x²+4�����ֽ���ʽ���ʴ�ѡ�����
D. x²?1=(x+1)(x?1)������ƽ�����ʽ�ֽ⣬�ʴ�ѡ����ȷ��
��ѡ��D.
D
��������A. x²+x=x(x+1)������ȡ����ʽ���ֽ���ʽ���ʴ�ѡ�����
B. x²+8x+16=(x+4)²���ǹ�ʽ���ֽ���ʽ���ʴ�ѡ�����
C. x²+4�����ֽ���ʽ���ʴ�ѡ�����
D. x²?1=(x+1)(x?1)������ƽ�����ʽ�ֽ⣬�ʴ�ѡ����ȷ��
��ѡ��D.