题目内容
下列各式中，能用平方差公式因式分解的是（ ）
A. x2+x B. x2+8x+16 C. x2+4 D. x2﹣1
D
【解析】A. x²+x=x(x+1)，是提取公因式法分解因式，故此选项错误；
B. x²+8x+16=(x+4)²，是公式法分解因式，故此选项错误；
C. x²+4，无法分解因式，故此选项错误；
D. x²?1=(x+1)(x?1)，能用平方差公因式分解，故此选项正确。
故选：D.
练习册系列答案
名校通行证有效作业系列答案
相关题目
如图，已知二次函数y=ax2+bx+8（a≠0）的图象与x轴交于点A（﹣2，0），
B（4，0）与y轴交于点C．
（Ⅰ）求抛物线的解析式及其顶点D的坐标；
（Ⅱ）求△BCD的面积；
（Ⅲ）若直线CD交x轴与点E，过点B作x轴的垂线，交直线CD与点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点．试探究抛物线最多可以向上平移多少个单位长度（直接写出结果，不写求解过程）．
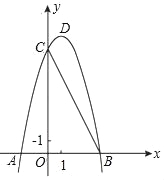
（Ⅰ）抛物线的解析式：y=﹣x2+2x+8=﹣（x﹣1）2+9，顶点D（1，9）；（Ⅱ）6；（Ⅲ）72.
【解析】
试题分析：（Ⅰ）利用待定系数法求出抛物线的解析式，通过对解析式进行配方能得到顶点D的坐标；
（Ⅱ）先求出直线BC解析式，进而用三角形的面积公式即可得出结论．
（Ⅲ）首先确定直线CD的解析式以及点E，F的坐标，若抛物线向上平移，首先表示出平移后的函数解析式；当x... △ABC中，AB＝5，BC＝3，则中线BD的取值范围是_________．
1＜BD＜4
【解析】延长BD到E，使BD=DE，连接AE，如图：
∵BD是△ABC中线，
∴AD=DC，
在△BDC和△EDA中，
∵，
∴△BDC≌△EDA.
∴BC=AE=3，
∵在△ABE中，根据三角形的三边关系定理得：5+3＞BE＞5-3，
∴2＜2BD＜8，
即1＜BD＜4.
故答案为：1＜BD＜4. 已知a+b=3，ab=2，求代数式a3b+2a2b2+ab3的值．
18
【解析】试题分析：先提取公因式ab，再根据完全平方公式进行二次分解，然后代入数据进行计算即可得解．
【解析】
a3b+2a2b2+ab3
=ab（a2+2ab+b2）
=ab（a+b）2，
将a+b=3，ab=2代入得，ab（a+b）2=2×32=18．
故代数式a3b+2a2b2+ab3的值是18． 分解因式：x2－4＝_____.
(x+2) (x-2)
【解析】试题解析：x2-4=（x+2）（x-2）． 已知二次函数的图象以A（-1，4）为顶点，且过点B（2，-5）．
（1）求该二次函数的解析式；
（2）求该二次函数图象与坐标轴的交点坐标；
（1）二次函数的关系式是y=-（x+1）2+4；（2）交点坐标是（-3，0）、（1，0）
【解析】试题分析：
（1）由题意可设二次函数解析式为，代入点B的坐标（2，-5）求出的值，即可得到二次函数的解析式；
（2）在（1）中所求函数解析式中，由时，求得对应的函数值即可得到函数图象与轴的交点坐标；由可得一元二次方程，解方程即可求得二次函数的图象与轴的交点坐标.
试题解析：
... 如果函数y=（k-3）
+kx+1是二次函数，那么k的值一定是 ．
0．
【解析】试题解析：由题意得：k2-3k+2=2，
解得k=0或k=3；
又∵k-3≠0，
∴k≠3．
∴当k=0时，这个函数是二次函数． 在第一象限内作射线OC，与x轴的夹角为60°，在射线OC上取一点A，过点A作AH⊥x 轴于点H，在抛物线y=x2（x＞0）上取一点P，在y轴上取一点Q，使得以P、O、Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是______．
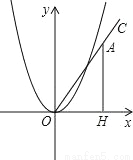
【解析】试题解析：①如图1，当∠POQ=∠OAH=30°，若以P，O，Q为顶点的三角形与△AOH全等，那么A、P重合；
∵∠AOH=60°，
∴直线OA：y=x，
联立抛物线的解析式得： ，
解得： 或，
故A（，3）；
②当∠POQ=∠AOH=60°，此时△POQ≌△AOH，
易知∠POH=30°，则直线y=x，联立抛物线的解析式，得： ，
解得：... 平行四边形的周长等于56 cm，两邻边长的比为3∶1，那么这个平行四边形较长的边长为_______.
21cm
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB=CD，AD=BC．
∵平行四边形的周长等于56cm，∴AB+CD+AD+BC=56cm，∴AB+BC=28cm．
∵BC：AB=3：1，∴BC=21cm，AB=7cm，∴这个平行四边形较长的边长为21cm．
故答案为：21cm．