��Ŀ����
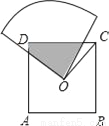
��ͼ��O�DZ߳�Ϊa��������ABCD�����ģ���һ��뾶�㹻����Բ��Ϊֱ�ǵ�����ֽ���Բ�ķ���O�㴦������ֽ���Բ����O��ת����������ABCD��ֽ�帲�Dz��ֵ����Ϊ��������
A.  a2 B.
a2 B.  a2 C.
a2 C.  a2 D.
a2 D. 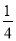 a
a
 B
����������������
���εİ뾶��AD��E����CD��F������OD����ͼ��
���ı���ABCDΪ�����Σ���OD=OC����COD=90�㣬��ODA=��OCD=45�㣮
�ߡ�EOF=90�㣬����EOD+��DOF=90�㣬��DOF+��COF=90�㣬���EOD=��FOC��
�ڡ�ODE�͡�OCF�У��ߡ�ODE=��OCF��OD=OC����EOD=��COF�����ODE�ա�OCF����S��OD...
B
����������������
���εİ뾶��AD��E����CD��F������OD����ͼ��
���ı���ABCDΪ�����Σ���OD=OC����COD=90�㣬��ODA=��OCD=45�㣮
�ߡ�EOF=90�㣬����EOD+��DOF=90�㣬��DOF+��COF=90�㣬���EOD=��FOC��
�ڡ�ODE�͡�OCF�У��ߡ�ODE=��OCF��OD=OC����EOD=��COF�����ODE�ա�OCF����S��OD...
 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д���ͬһ����ϵ�У�һ�κ���y=ax+b����κ���y=ax2+b�Ĵ���ͼ���ǣ�������
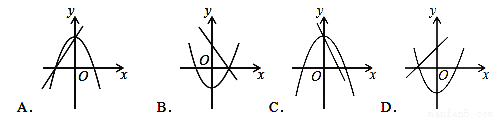
A. A B. B C. C D. D
 C
���������⣺A����һ�κ���y=ax+b��ͼ��ɵã�a��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������ϣ���A����
B����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��B����
C����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��C��ȷ��...
C
���������⣺A����һ�κ���y=ax+b��ͼ��ɵã�a��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������ϣ���A����
B����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��B����
C����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��C��ȷ��... �����¼��У���������¼����ǣ�������
A. ͨ��ˮ���ȵ�100��ʱ����
B. ����Т��ij���������£����Ϊ��150��
C. һ������װ��5������������һ���Ǻ���
D. �����Ա�ڷ�������Ͷ��һ�Σ�δͶ��
 D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD.
D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD. ��ͼ���ӵ�����ֱ�����׳�һ��С��С��ĸ߶�h����λ��m����С���˶�ʱ��t����λ��s��֮��Ĺ�ϵʽΪh=30t-5t2����ôС����׳������䵽��������Ҫ��ʱ���ǣ�������
A. 6s B. 4s C. 3s D. 2s
 A
�������������������С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2����h=0����õ���ֵ֮�������Ҫ��õĽ����
��С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2�� ��h=0����5t2+30t=0 ��ã�t1=0��t2=6
��t=6��С����׳������䵽��������Ҫ��ʱ����6�룮
A
�������������������С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2����h=0����õ���ֵ֮�������Ҫ��õĽ����
��С��߶�h���˶�ʱ��t�Ĺ�ϵʽh=30t��5t2�� ��h=0����5t2+30t=0 ��ã�t1=0��t2=6
��t=6��С����׳������䵽��������Ҫ��ʱ����6�룮 ��ͼ����Rt��ABC�Ƶ�A��ʱ����ת40�㣬�õ�Rt��AB��C�䣬��C��ǡ�����ڱ�AB�ϣ�����BB�䣬���BB��C��=________�ȣ�
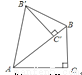
 20��
�����������������������תͼ�οɵá�B��AB=40�㣬AB=AB�䣬���B��BA=70�㣬���ݡ�BCB��=90��ɵá�BB��C=90�㣭70��=20��.
20��
�����������������������תͼ�οɵá�B��AB=40�㣬AB=AB�䣬���B��BA=70�㣬���ݡ�BCB��=90��ɵá�BB��C=90�㣭70��=20��. ����A(3��2)��x������ƽ��4����λ���ȵõ���A�䣬���A�����ԭ��ԳƵĵ��������( )
A. (-3��2) B. (-1��2) C. (1��2) D. (1��-2)
 D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD��
D
���������������������A��3��2������ƽ��4����λ���ȵõ�A�䣬�ɵõ�A�������Ϊ����1��2�������Ե�A�����y��ԳƵĵ�������ǣ�1��2������ѡD�� ��ͼ����֪���κ���y=ax2+bx+8��a��0����ͼ����x�ύ�ڵ�A����2��0����
B��4��0����y�ύ�ڵ�C��
�����������ߵĽ���ʽ���䶥��D�����ꣻ
�������BCD�������
������ֱ��CD��x�����E������B��x��Ĵ��ߣ���ֱ��CD���F��������������Գ�������ƽ�ƣ�ʹ���������߶�EF���й����㣮��̽������������������ƽ�ƶ��ٸ���λ���ȣ�ֱ��д���������д�����̣���
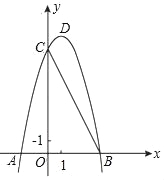
 ���������ߵĽ���ʽ��y=��x2+2x+8=����x��1��2+9������D��1��9��������6������72.
��������
����������������ô���ϵ������������ߵĽ���ʽ��ͨ���Խ���ʽ�����䷽�ܵõ�����D�����ꣻ
���������ֱ��BC����ʽ�������������ε������ʽ���ɵó����ۣ�
��������ȷ��ֱ��CD�Ľ���ʽ�Լ���E��F�����꣬������������ƽ�ƣ����ȱ�ʾ��ƽ�ƺ�ĺ�������ʽ����x...
���������ߵĽ���ʽ��y=��x2+2x+8=����x��1��2+9������D��1��9��������6������72.
��������
����������������ô���ϵ������������ߵĽ���ʽ��ͨ���Խ���ʽ�����䷽�ܵõ�����D�����ꣻ
���������ֱ��BC����ʽ�������������ε������ʽ���ɵó����ۣ�
��������ȷ��ֱ��CD�Ľ���ʽ�Լ���E��F�����꣬������������ƽ�ƣ����ȱ�ʾ��ƽ�ƺ�ĺ�������ʽ����x... ��ͼ����a��0��b��0��c��0����������y=ax2+bx+c�Ĵ���ͼ��Ϊ��������
A. 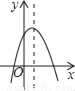 B.
B. 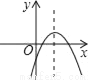 C.
C. 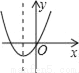 D.
D. 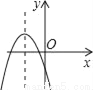
 B
�������������������a��0��
�������ߵĿ��ڷ������£�
�ʵ�����ѡ�����
��c��0��
����������y��Ľ���Ϊ��y��ĸ������ϣ�
�ʵ�һ��ѡ�����
��a��0��b��0���Գ���Ϊx=��0��
��Գ�����y���Ҳ࣬
�ʵ��ĸ�ѡ�����
��ѡB��
B
�������������������a��0��
�������ߵĿ��ڷ������£�
�ʵ�����ѡ�����
��c��0��
����������y��Ľ���Ϊ��y��ĸ������ϣ�
�ʵ�һ��ѡ�����
��a��0��b��0���Գ���Ϊx=��0��
��Գ�����y���Ҳ࣬
�ʵ��ĸ�ѡ�����
��ѡB�� ��֪a+b=3��ab=2�������ʽa3b+2a2b2+ab3��ֵ��
 18
���������������������ȡ����ʽab���ٸ�����ȫƽ����ʽ���ж��ηֽ⣬Ȼ��������ݽ��м��㼴�ɵý⣮
��������
a3b+2a2b2+ab3
=ab��a2+2ab+b2��
=ab��a+b��2��
��a+b=3��ab=2����ã�ab��a+b��2=2��32=18��
�ʴ���ʽa3b+2a2b2+ab3��ֵ��18��
18
���������������������ȡ����ʽab���ٸ�����ȫƽ����ʽ���ж��ηֽ⣬Ȼ��������ݽ��м��㼴�ɵý⣮
��������
a3b+2a2b2+ab3
=ab��a2+2ab+b2��
=ab��a+b��2��
��a+b=3��ab=2����ã�ab��a+b��2=2��32=18��
�ʴ���ʽa3b+2a2b2+ab3��ֵ��18�� 
