题目内容
如图，教练对小明推铅球的录像进行技术分析，发现铅球行进高度y(m)与水平距离x(m)之间的关系为y＝－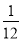
(x－4)2＋3，由此可知铅球推出的距离是___________.
10
【解析】【解析】
在中，令y=0，得，解得：x1=10，x2=﹣2（舍去），即铅球推出的距离是10m．故答案为：10．
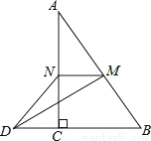
如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=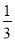
BD，连接DM、DN、MN．若AB=6，则DN=___．
3．
【解析】试题分析：连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，又CD=BD，可得MN=CD，又由MN∥BC，可得四边形DCMN是平行四边形，所以DN=CM，根据直角三角形的性质得到CM=AB=3，即可得DN=3． 如图，在△ABC中，AB=4，BC=6，DE、DF是△ABC的中位线，则四边形BEDF的周长是（ ）
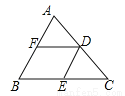
A．5 B．7 C．8 D．10
D．
【解析】
试题分析：∵AB=4，BC=6，DE、DF是△ABC的中位线，∴DE=AB=2，DF=BC=3，DE∥BF，DF∥BE，∴四边形BEDF为平行四边形，∴四边形BEDF的周长为：2×2+3×2=10，故选D． 在同一坐标系中，一次函数y=ax+b与二次函数y=ax2+b的大致图象是（ ）
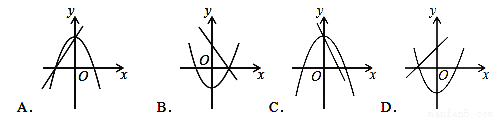
A. A B. B C. C D. D
C
【解析】解：A．由一次函数y=ax+b的图象可得：a＞0，此时二次函数y=ax2+b的图象应该开口向上，故A错误；
B．由一次函数y=ax+b的图象可得：a＜0，b＞0，此时二次函数y=ax2+b的图象应该开口向下，顶点的纵坐标大于零，故B错误；
C．由一次函数y=ax+b的图象可得：a＜0，b＞0，此时二次函数y=ax2+b的图象应该开口向下，顶点的纵坐标大于零，故C正确；... 抛物线y=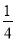
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点，过点A作直线AC⊥x轴，交直线y=2x于点C.
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.
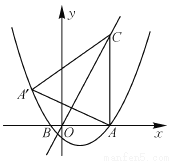
（1）．（2）点A/的坐标为（﹣3,4）．点A/在该抛物线上．（3）点P运动到时，四边形PACM是平行四边形．
【解析】试题分析：（1）将点A、B的坐标代入抛物线的解析式，得到关于b、c的二元一次方程组，从而可解得b、c的值；
（2）过点B′作B′E⊥x轴于E，BB′与OC交于点F．由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2，将x=2代入直线y=﹣2x的解析式可求得点C的坐... 如图，正方形ABCD中，AB＝8cm，对角线AC、BD相交于点O，点E、F分别从B、C两点同时出发，以1cm/s的速度沿BC、CD运动，到点C、D时停止运动，设运动时间为t(s)，△OEF的面积为S(cm2)，则S(cm2)与t(s)的函数关系可用图象表示为( )
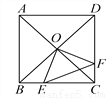
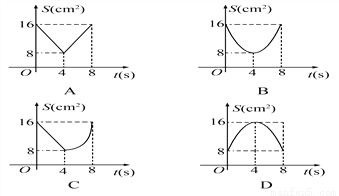
A. A B. B C. C D. D
B
【解析】试题分析：由点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，得到BE=CF=t，则CE=8﹣t，再根据正方形的性质得OB=OC，∠OBC=∠OCD=45°，然后根据“SAS”可判断△OBE≌△OCF，所以S△OBE=S△OCF，这样S四边形OECF=S△OBC=16，于是S=S四边形OECF﹣S△CEF=16﹣（8﹣t）t，然后配方得到S=（t﹣4）2+8（... 从1，2，3，4，5这五个数中任意取两个相乘，问：
（1）积为偶数，属于哪类事件？有几种可能情况？
（2）积为奇数，属于哪类事件？有几种可能情况？
（3）积为无理数，属于哪类事件？
（1）可能事件，7；（2）可能事件，3；（3）不可能事件
【解析】试题分析：（1），（2）由于五个数中任意取两数相乘有奇数有偶数，所以（1）（2）都为不确定事件，分别写出乘积为偶数与为奇数的情况，即可看出分别有几种情况．
（3）由于五个数都是有理数，他们的乘积也一定为有理数，不可能为无理数，所以（3）为不可能事件．
试题解析： 取任意两个数相乘，可能的结果如下表所示（重复的不留在表中... 下列事件中，属于随机事件的是（ ）
A. 通常水加热到100℃时沸腾
B. 测量孝感某天的最低气温，结果为﹣150℃
C. 一个袋中装有5个黑球，从中摸出一个是黑球
D. 篮球队员在罚球线上投篮一次，未投中
D
【解析】试题解析：结合所学的随机事件与必然事件的意义，A必然发生，是必然事件；B一定不会发生，是必然事件；C一定会发生，是必然事件；D 罚球投篮一次未投中是可能发生的，属于随机事件.故选D. 如图，已知二次函数y=ax2+bx+8（a≠0）的图象与x轴交于点A（﹣2，0），
B（4，0）与y轴交于点C．
（Ⅰ）求抛物线的解析式及其顶点D的坐标；
（Ⅱ）求△BCD的面积；
（Ⅲ）若直线CD交x轴与点E，过点B作x轴的垂线，交直线CD与点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点．试探究抛物线最多可以向上平移多少个单位长度（直接写出结果，不写求解过程）．
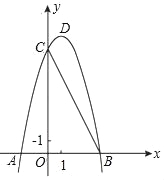
（Ⅰ）抛物线的解析式：y=﹣x2+2x+8=﹣（x﹣1）2+9，顶点D（1，9）；（Ⅱ）6；（Ⅲ）72.
【解析】
试题分析：（Ⅰ）利用待定系数法求出抛物线的解析式，通过对解析式进行配方能得到顶点D的坐标；
（Ⅱ）先求出直线BC解析式，进而用三角形的面积公式即可得出结论．
（Ⅲ）首先确定直线CD的解析式以及点E，F的坐标，若抛物线向上平移，首先表示出平移后的函数解析式；当x...