题目内容
一个图形无论经过平移变换，还是经过旋转变换，下列说法正确的是（ ）
①对应线段平行
②对应线段相等
③图形的形状和大小都没有发生变化
④对应角相等．
A. ①②③ B. ②③④ C. ①②④ D. ①③④
B
【解析】【解析】
①平移后对应线段平行，旋转对应线段不一定平行，故本小题错误；
②无论平移还是旋转，对应线段相等，故本小题正确；
③无论平移还是旋转，图形的形状和大小都没有发生变化，故本小题正确；
④无论平移还是旋转，对应角相等，故本小题正确．
综上所述，说法正确的是②③④．
故选B．
抛物线y=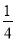
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点，过点A作直线AC⊥x轴，交直线y=2x于点C.
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.
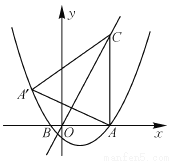
（1）．（2）点A/的坐标为（﹣3,4）．点A/在该抛物线上．（3）点P运动到时，四边形PACM是平行四边形．
【解析】试题分析：（1）将点A、B的坐标代入抛物线的解析式，得到关于b、c的二元一次方程组，从而可解得b、c的值；
（2）过点B′作B′E⊥x轴于E，BB′与OC交于点F．由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2，将x=2代入直线y=﹣2x的解析式可求得点C的坐... 如图，三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小都相同，正常水位时，大孔水面宽度AB=20m，顶点M距水面6m（即MO=6m），小孔顶点N距水面4.5m（即NC=4.5m），当水位上涨刚好淹没小孔时，借助图中的直角坐标系，求此时大孔的水面宽度EF．
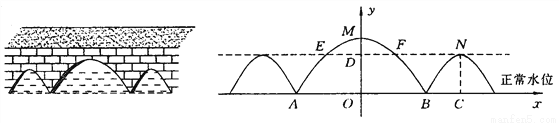
水面宽度为10m
【解析】试题分析:设大孔抛物线的解析式为一般式形式,把点A(－10,0)代入解析式解得a=,因此函数解析式为,再由NC=4.5,可知点E,F的纵坐标,代入解析式即可求出点E,F的横坐标,继而可以求出EF.
试题解析:设抛物线的解析式为y=ax2+6,依题意得:B（10,0）,
∴a×102+6=0,解得a=－0.06,即y=－0.06x2+6,
当y=4.... 如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=________度．
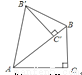
20°
【解析】试题分析：根据旋转图形可得∠B′AB=40°，AB=AB′，则∠B′BA=70°，根据∠BCB′=90°可得∠BB′C=90°－70°=20°. 如图，在△ABC中，∠CAB=70°．在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（ ）
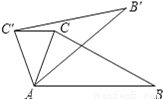
A. 30° B. 35° C. 40° D. 50°
C
【解析】∵CC′∥AB，
∴∠C′CA=∠CAB=70°.
∵△AB′C′是由△ABC绕点A旋转得到的，
∴AC′=AC，∠C′AB′=∠CAB，
∴∠AC′C=∠ACC′=70°，∠C′AB′-∠CAB′=∠CAB-∠CAB′，即∠CAC′=∠BAB′，
∴∠CAC′=180°-70°-70°=40°，
∴∠BAB′=40°.
故选C.
... 如图，已知二次函数y=ax2+bx+8（a≠0）的图象与x轴交于点A（﹣2，0），
B（4，0）与y轴交于点C．
（Ⅰ）求抛物线的解析式及其顶点D的坐标；
（Ⅱ）求△BCD的面积；
（Ⅲ）若直线CD交x轴与点E，过点B作x轴的垂线，交直线CD与点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点．试探究抛物线最多可以向上平移多少个单位长度（直接写出结果，不写求解过程）．
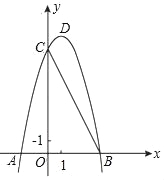
（Ⅰ）抛物线的解析式：y=﹣x2+2x+8=﹣（x﹣1）2+9，顶点D（1，9）；（Ⅱ）6；（Ⅲ）72.
【解析】
试题分析：（Ⅰ）利用待定系数法求出抛物线的解析式，通过对解析式进行配方能得到顶点D的坐标；
（Ⅱ）先求出直线BC解析式，进而用三角形的面积公式即可得出结论．
（Ⅲ）首先确定直线CD的解析式以及点E，F的坐标，若抛物线向上平移，首先表示出平移后的函数解析式；当x... 如图，抛物线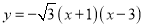
与x轴交于A、B两点，与y轴交于点C，点D为该抛物线的对称轴上一点，当点D到直线BC和到x轴的距离相等时，则点D的坐标为 ．
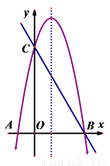
或
【解析】试题分析：如图所示：
∵抛物线y=﹣（x+1）（x﹣3）与x轴交于A、B两点，与y轴交于点C，
∴当﹣（x+1）（x﹣3）=0时，x=﹣1，或x=3，
当x=0时，y=3，
∴A（﹣1，0），B（3，0），C（0，3），对称轴x=1，
∴BM=3﹣1=2，
当点D到直线BC和到x轴的距离相等时，点D在∠ABC或∠ABE的平分线上，
①点D... 如图，已知△ABC中，AB=AC，周长为24，AC边上的中线BD把△ABC分成周长差为6的两个三角形，则△ABC各边的长分别为多少？
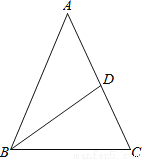
三角形的各边长为10、10、4
【解析】试题分析：分AB＞BC和AB＜BC两种情况求得AB、BC的长，再由三角形的三边关系进行取舍即可.
试题解析：
根据题意结合图形，分成两部分的周长的差等于腰长与底边的差，
（1）若AB＞BC，则AB-BC=6，
又因为2AB+BC=24，
联立方程组并求解得：AB=10，BC=4，
10、10、4三边能够组成三角形；
... 分解因式：x2－4＝_____.
(x+2) (x-2)
【解析】试题解析：x2-4=（x+2）（x-2）．