题目内容
6.如图,有一个长方形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED剪下沿DB方向平移.使DE与BC边重合,若AE边与DE边相交于点F,则△ADF的面积为2.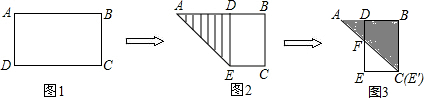
分析 根据折叠易得BD,AB长,利用相似可得FF长,
解答 解:由折叠的性质知,第二个图中BD=AB-AD=4,第三个图中AD=AB-BD=2,
∵BC∥DF,
∴BC:DF=AB:AD,
即4:DF=4:2,
∴DF=2,
∴△ADF的面积=$\frac{1}{2}$AD•DF=2;
故答案为:2.
点评 此题考查折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,相似三角形的判定与性质,三角形的面积公式等知识点.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.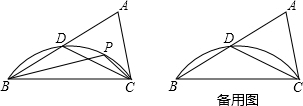
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0). 已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.
已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.