题目内容
16．
已知，如图?ABCD中，E为AD边上的一点，AE：ED=2：5，连结AC、BE交于点F，若AC=20cm，则AF=$\frac{40}{9}$，CF=$\frac{140}{9}$．
分析 根据“AE：ED=2：5”求出AE：AD即AE：BC的值是2：7，再根据相似三角形对应边成比例求出AF与FC的比，又AC=20，所以AF，CF便不难求出．
解答 解：∵AE：ED=2：5，
∴AE：AD=2：7，
在平行四边形ABCD中，AD=BC，AD∥BC，
∴△AEF∽△CBF，
∴AF：FC=AE：BC=2：7，
∵AC=20，
∴AF=$\frac{2}{2+7}$×20=$\frac{40}{9}$，
∴CF=AC-AF=$\frac{140}{9}$，
故答案为：$\frac{40}{9}$，$\frac{140}{9}$．
点评 本题考查了相似三角形的判定和性质，平行四边形的性质，比例式的变形是解题的关键．
练习册系列答案
优加精卷系列答案
相关题目
11．在“母亲节”期间，某校部分团员参加社会公益活动，准备构建一批许愿瓶进行销售，并将所得利润捐给慈善机构，根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如表所示：
（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；为了方便顾客，售价定位多少时可获利1200元；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定此时的销售单价，并求出此时的最大利润．
（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；为了方便顾客，售价定位多少时可获利1200元；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定此时的销售单价，并求出此时的最大利润．
| z（元/个） | 16 | 14 | 12 | 10 |
| y（个） | 120 | 180 | 240 | 300 |
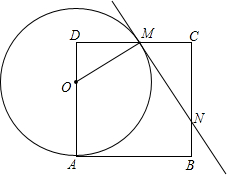如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作⊙O的切线交边BC于N．