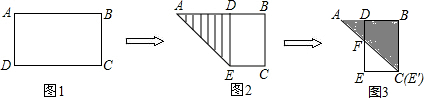
题目内容
9. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.
分析 首先证明△DBE≌△ECF,进而得到∠EFC=∠DEB,再根据三角形内角和计算出∠CFE+∠FEC的度数,进而得到∠DEB+∠FEC的度数,然后可算出∠DEF的度数.
解答 解:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,
$\left\{\begin{array}{l}{BD=EC}\\{∠B=∠C}\\{EB=CF}\end{array}\right.$,
∴△DBE≌△ECF(SAS),
∴∠EFC=∠DEB,
∵∠A=50°,
∴∠C=(180°-50°)÷2=65°,
∴∠CFE+∠FEC=180°-65°=115°,
∴∠DEB+∠FEC=115°,
∴∠DEF=180°-115°=65°,
故答案为:65°.
点评 本题考查了全等三角形的性质和判定,以及三角形内角和的定理,关键是熟练掌握三角形内角和是180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.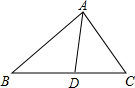 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )| A. | 3:4 | B. | 4:3 | C. | 16:9 | D. | 9:16 |
 在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.
在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.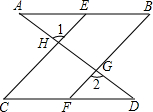 完成下面的证明过程:
完成下面的证明过程: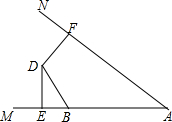 如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.



 小王在一路灯下A、C两点的影长AB、CD如图所示.
小王在一路灯下A、C两点的影长AB、CD如图所示.